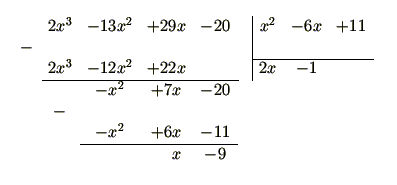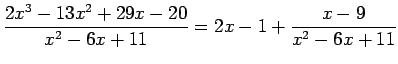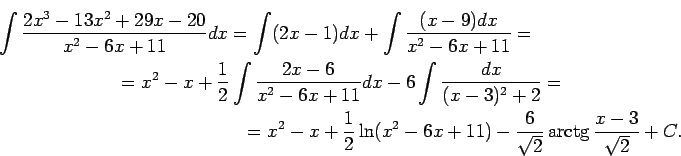Apskata šāda veida integrāļus:
Apskata šāda veida integrāļus:
![]() , kur
, kur ![]() ir racionāla
funkcija. Katru racionālu funkciju var izteikt kā divu polinomu
attiecību, t.i.,
ir racionāla
funkcija. Katru racionālu funkciju var izteikt kā divu polinomu
attiecību, t.i.,
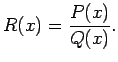
Ja daļa
![]() nav īsta, t.i., skaitītāja pakāpe nav
zemāka (vienāda vai lielāka) par saucēja pakāpi, tad šādu daļu
var izteikt kā kaut kāda polinoma un īstas daļas summu.
nav īsta, t.i., skaitītāja pakāpe nav
zemāka (vienāda vai lielāka) par saucēja pakāpi, tad šādu daļu
var izteikt kā kaut kāda polinoma un īstas daļas summu.
Apskata īstu daļu
![]() ir šī polinoma reālās saknes,
ir šī polinoma reālās saknes,
![]() ,
,
![]() - reāli skaitļi,
- reāli skaitļi,
![]() ,
,
![]() - naturāli skaitļi
(atbilstošo
sakņu kārtas),
- naturāli skaitļi
(atbilstošo
sakņu kārtas),
pie tam
![]() un
kvadrāttrinomiem
un
kvadrāttrinomiem
![]() nav reālu
sakņu.
nav reālu
sakņu.
Īstu daļu var izteikt šādi:
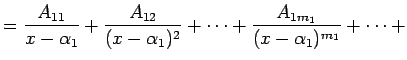 |
||
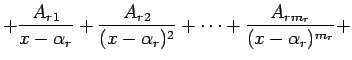 |
||
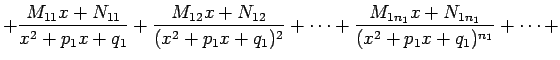 |
||
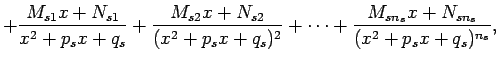 |
![]() ,
,
![]() ,
,
![]()
ir reāli skaitļi, kurus atrod ar nenoteikto koeficientu
metodi. Parasti koeficientus apzīmē ar burtiem ![]() utt.
utt.
Piemēram,
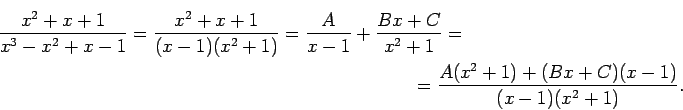
Seko, ka
Pielīdzina polinomu koeficientus pie ![]() vienādām pakāpēm un iegūst
šādu vienādojumu sistēmu:
vienādām pakāpēm un iegūst
šādu vienādojumu sistēmu:
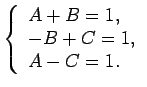
Šīs sistēmas atrisinājums ir
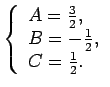
Tādējādi
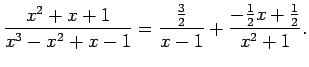
Vienādojumu sistēmu var arī iegūt, ja vienādībā
Apskata vēl vienu daļu.
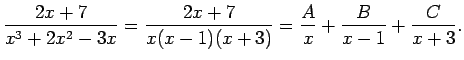
Seko, ka
Argumenta vietā ievieto vērtības ![]() ,
, ![]() ,
, ![]() un iegūst, ka
un iegūst, ka
![]() ,
,
![]() ,
,
![]() .
.
Tādējādi
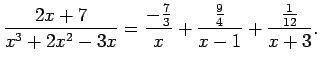
Izteiksmes
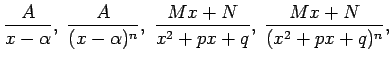
Jebkurā intervālā, kas nesatur
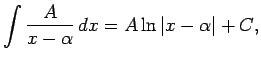
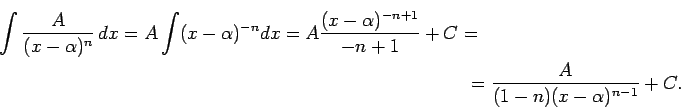
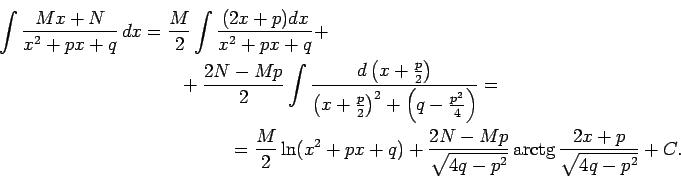
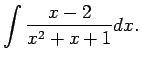
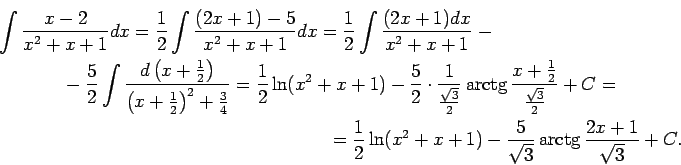
Integrāļa
![]() atrašana ir diezgan
sarežģīta. Virpirms apskata integrāli
atrašana ir diezgan
sarežģīta. Virpirms apskata integrāli
![]() (
(
![]() ,
,
![]() ,
, ![]() ).
).
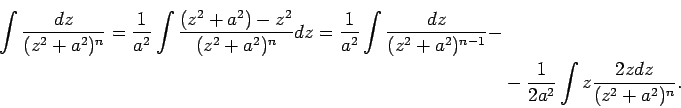
Integrāļa
![]() atrašanai pielieto
parciālās integrēšanas formulu.
atrašanai pielieto
parciālās integrēšanas formulu.
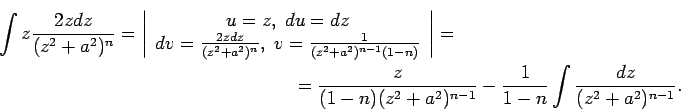
Tātad
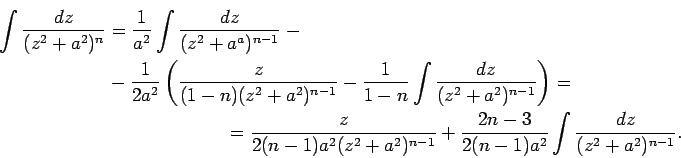
Tika iegūta formula, kuru sauc par rekurences formulu. Šī
formula integrāļa
![]() izskaitļošanu
reducē uz integrāļa
izskaitļošanu
reducē uz integrāļa
![]() izskaitļošanu.
izskaitļošanu.
Piemēram, pie
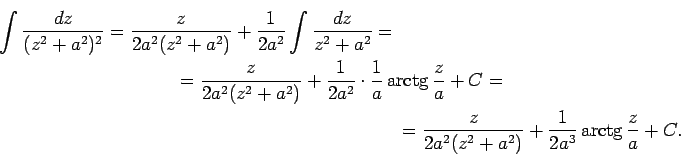
Visbeidzot
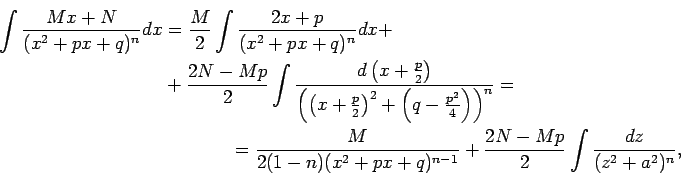
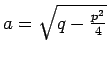 .
.
Integrāli
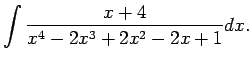
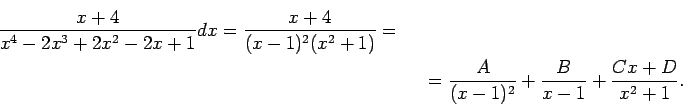
Ievieto ![]() , iegūst
, iegūst
![]() . Pārējos koeficientus atrod,
pielīdzinot koeficientus pie vienādām
. Pārējos koeficientus atrod,
pielīdzinot koeficientus pie vienādām ![]() pakāpēm. Iegūst, ka
pakāpēm. Iegūst, ka
![]() ,
, ![]() ,
,
![]() .
.
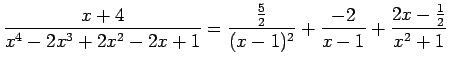
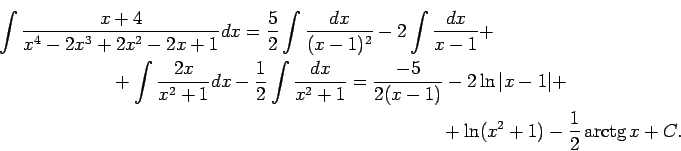
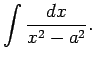
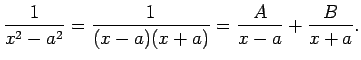 |
|
Argumenta vietā ievieto ![]() un
un ![]() . Iegūst, ka
. Iegūst, ka
![]() un
un
![]() .
.
Tādējādi
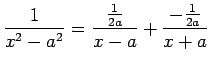
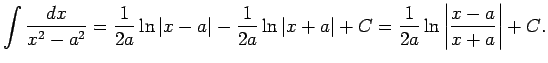
Arī šo integrāli pievieno pamatintegrāļu tabulai.
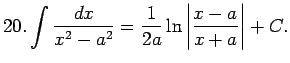
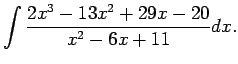
Daļa nav īsta, tāpēc vispirms skaitītāja polinomu dalot ar saucēja polinomu, atdala veselo daļu.