


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.7. Trigonometrisko funkciju integrēšana
Augstāk: 1. NENOTEIKTAIS INTEGRĀLIS
Iepriekšējais: 1.5. Racionālu funkciju integrēšana
Apskata tādas iracionālas funkcijas, kuras ar mainīgā
aizvietošanu var reducēt uz racionālām funkcijām.
- Integrālis
![$ \int R\left(x, \sqrt[n]{\frac{ax+b}{cx+d}}\right)dx$](img264.gif) .
.
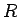 ir racionāla argumentu
ir racionāla argumentu 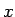 un
un
![$ \sqrt[n]{\frac{ax+b}{cx+d}}$](img265.gif) funkcija,
funkcija,
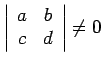 ,
, 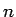 ir naturāls skaitlis.
ir naturāls skaitlis.
kur 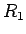 ir argumenta
ir argumenta 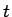 racionāla funkcija.
racionāla funkcija.
-
1.17. piemērs.
- Atrast
-
1.18. piemērs.
- Atrast
Zemintegrāļa funkcija ir racionāla attiecībā pret argumentu
![$ \sqrt[6]{2x+1}$](img272.gif) , tāpēc to apzīmē ar jaunu mainīgo
, tāpēc to apzīmē ar jaunu mainīgo 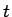 .
.
- Integrālis
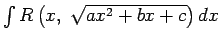 .
.
Arī šoreiz 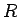 ir racionāla savu argumentu funkcija. Šo integrāli,
izdarot mainīgā aizvietošanu, var reducēt uz integrāli no
racionālas funkcijas. Tam nolūkam lieto vienu no tā saucamajām
Eilera substitūcijām. Substitūcijas izvēle atkarīga no
skaitļiem
ir racionāla savu argumentu funkcija. Šo integrāli,
izdarot mainīgā aizvietošanu, var reducēt uz integrāli no
racionālas funkcijas. Tam nolūkam lieto vienu no tā saucamajām
Eilera substitūcijām. Substitūcijas izvēle atkarīga no
skaitļiem 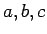 .
.
Eilera pirmā substitūcija.
Ja 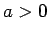 , tad apzīmē
, tad apzīmē
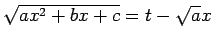 .
.
kur 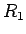 ir argumenta
ir argumenta 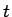 racionāla funkcija.
racionāla funkcija.
Eilera otrā substitūcija.
Ja 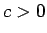 , tad apzīmē
, tad apzīmē
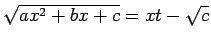 .
.
Arī šoreiz integrālis tiek reducēts uz integrāli no racionālas
funkcijas (Izdarīt to patstāvīgi).
Eilera trešā substitūcija.
Ja kvadrāttrinomam 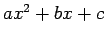 ir reālas un dažādas saknes
ir reālas un dažādas saknes 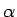 un
un 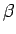 , tad apzīmē
, tad apzīmē
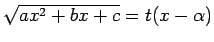 . Iegūst, ka
. Iegūst, ka
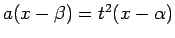 . Tātad
. Tātad
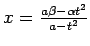 , utt.
, utt.
-
1.9. piezīme.
- Integrāļu
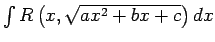 izskaitļošanai teorētiski pietiek ar Eilera pirmo un Eilera trešo
substitūciju (Pamatot to).
izskaitļošanai teorētiski pietiek ar Eilera pirmo un Eilera trešo
substitūciju (Pamatot to).
-
1.19. piemērs.
- Atrast
Šo integrāli pievieno pamatintegrāļu tabulai.
-
1.20. piemērs.
- Atrast
Šoreiz lieto Eilera trešo substitūciju. Kvadrāttrinoma 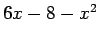 saknes ir
saknes ir 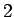 un
un 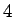 .
.
kur
- Integrālis
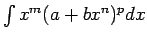 .
.
Izteiksmi
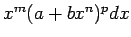 , kur
, kur 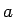 un
un 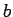 ir reāli skaitļi, bet
ir reāli skaitļi, bet
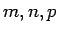 ir racionāli skaitļi, sauc par binomiālo
diferenciāli.
ir racionāli skaitļi, sauc par binomiālo
diferenciāli.
Krievu matemātiķis Čebiševs pierādīja, ka integrāli
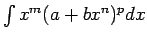 var izteikt ar elementārām funkcijām tikai trijos
gadījumos.
var izteikt ar elementārām funkcijām tikai trijos
gadījumos.
- 1. gadījums.
- Ja
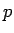 ir vesels skaitlis, tad
apzīmē
ir vesels skaitlis, tad
apzīmē 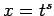 , kur
, kur 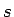 ir daļu
ir daļu 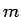 un
un 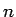 kopsaucējs.
kopsaucējs.
kur 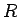 ir racionāla funkcija (
ir racionāla funkcija (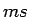 un
un 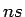 ir veseli skaitļi).
ir veseli skaitļi).
- 2. gadījums.
- Ja
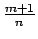 ir vesels skaitlis,
tad apzīmē
ir vesels skaitlis,
tad apzīmē
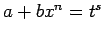 , kur
, kur 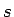 ir daļas
ir daļas 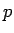 saucējs.
saucējs.
kur 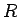 ir racionāla funkcija (
ir racionāla funkcija (
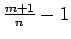 un
un 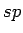 ir veseli
skaitļi).
ir veseli
skaitļi).
- 3. gadījums.
- Ja
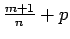 ir vesels
skaitlis, tad apzīmē
ir vesels
skaitlis, tad apzīmē
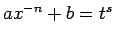 , kur
, kur 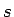 ir daļas
ir daļas 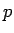 saucējs
(pamatot patstāvīgi).
saucējs
(pamatot patstāvīgi).
-
1.10. piezīme.
- Katrā no šiem gadījumiem pēc atbilstošās racionālās
funkcijas integrēšanas jāatgriežas pie iepriekšējā mainīgā
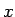 .
.
-
1.21. piemērs.
- Atrast
-
1.22. piemērs.
- Atrast



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.7. Trigonometrisko funkciju integrēšana
Augstāk: 1. NENOTEIKTAIS INTEGRĀLIS
Iepriekšējais: 1.5. Racionālu funkciju integrēšana
2002-11-06
![$ \int R\left(x, \sqrt[n]{\frac{ax+b}{cx+d}}\right)dx$](img264.gif) .
.
![$ \int R\left(x, \sqrt[n]{\frac{ax+b}{cx+d}}\right)dx$](img264.gif) .
.
![$ \sqrt[n]{\frac{ax+b}{cx+d}}$](img265.gif) funkcija,
funkcija,
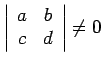 ,
, ![\begin{multline*}
\int R\left(x, \sqrt[n]{\frac{ax+b}{cx+d}}\right)dx=\left\vert...
...a},\;t\right)\frac{n(ad-bc)t^{n-1}}{(ct^n-a)^2}dt=\int
R_1(t)dt,
\end{multline*}](img267.gif)
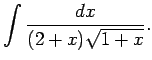
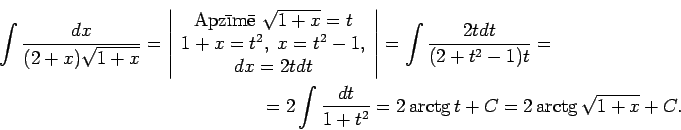
![$\displaystyle \int\frac{dx}{\sqrt[3]{(2x+1)^2}-\sqrt{2x+1}}\/.$](img271.gif)
![\begin{multline*}
\int\frac{dx}{\sqrt[3]{(2x+1)^2}-\sqrt{2x+1}}=
\int\frac{dx}{\...
...6]{2x+1}+1\right)^2+3\ln\left\vert\sqrt[6]{2x+1}-1\right\vert+C.
\end{multline*}](img273.gif)
![]() ir racionāla savu argumentu funkcija. Šo integrāli,
izdarot mainīgā aizvietošanu, var reducēt uz integrāli no
racionālas funkcijas. Tam nolūkam lieto vienu no tā saucamajām
Eilera substitūcijām. Substitūcijas izvēle atkarīga no
skaitļiem
ir racionāla savu argumentu funkcija. Šo integrāli,
izdarot mainīgā aizvietošanu, var reducēt uz integrāli no
racionālas funkcijas. Tam nolūkam lieto vienu no tā saucamajām
Eilera substitūcijām. Substitūcijas izvēle atkarīga no
skaitļiem ![]() .
.
![]() , tad apzīmē
, tad apzīmē
![]() .
.
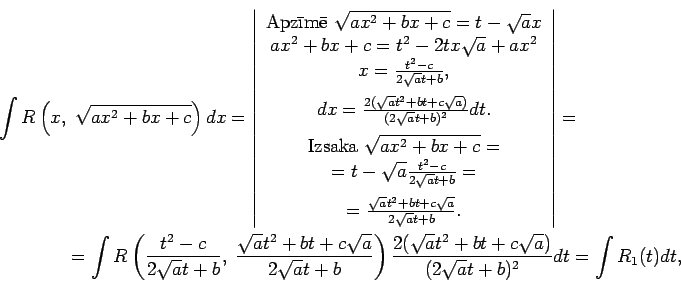
![]() , tad apzīmē
, tad apzīmē
![]() .
.
![]() ir reālas un dažādas saknes
ir reālas un dažādas saknes ![]() un
un ![]() , tad apzīmē
, tad apzīmē
![]() . Iegūst, ka
. Iegūst, ka
![]() . Tātad
. Tātad
![]() , utt.
, utt.
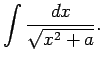

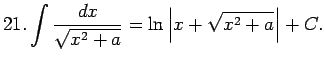
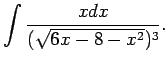
![]() saknes ir
saknes ir ![]() un
un ![]() .
.
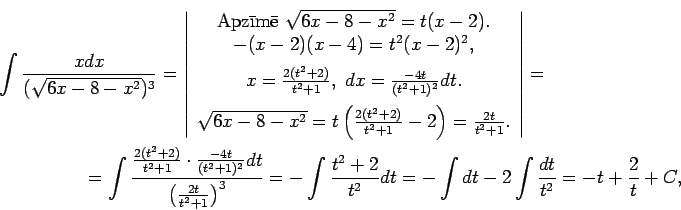
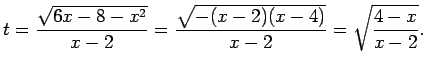
![]() , kur
, kur ![]() un
un ![]() ir reāli skaitļi, bet
ir reāli skaitļi, bet
![]() ir racionāli skaitļi, sauc par binomiālo
diferenciāli.
ir racionāli skaitļi, sauc par binomiālo
diferenciāli.
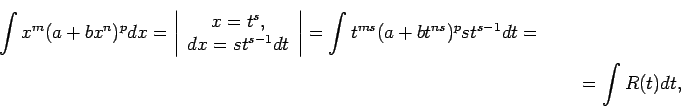
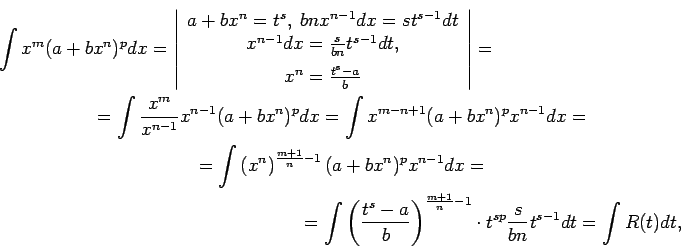
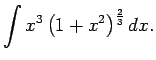
![\begin{multline*}
\int x^3\left(1+x^2\right)^\frac{2}{3}dx=\left\vert\begin{arra...
...ac{3}{16}\sqrt[3]{(1+x^2)^8}-\frac{3}{10}\sqrt[3]{(1+x^2)^5}+C.
\end{multline*}](img316.gif)
![$\displaystyle \int\frac{\sqrt[3]{(2x^3+1)^2}}{x^6}dx\/.$](img317.gif)
![\begin{multline*}
\int\frac{\sqrt[3]{(2x^3+1)^2}}{x^6}dx=\int
x^{-6}(1+2x^3)^\fr...
...{-3}+2)^5}+C=\\ =-\frac{1}{5}\frac{\sqrt[3]{(1+2x^3)^5}}{x^5}+C.
\end{multline*}](img318.gif)