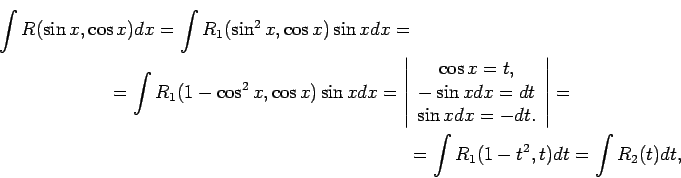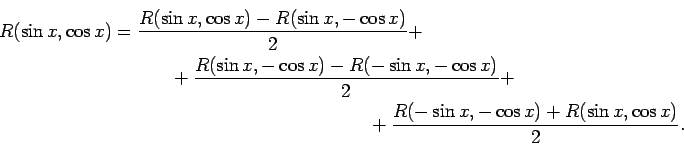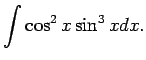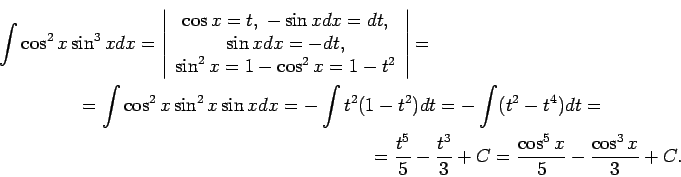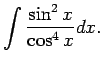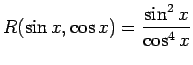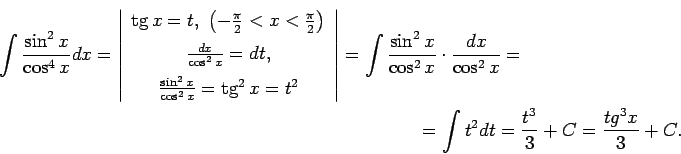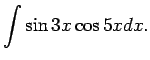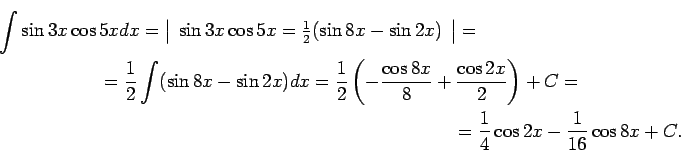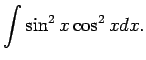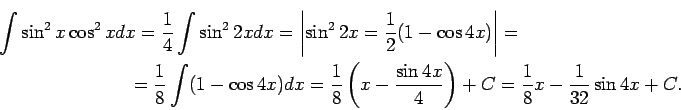Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.8. Jautājumi
Augstāk: 1. NENOTEIKTAIS INTEGRĀLIS
Iepriekšējais: 1.6. Iracionālu funkciju integrēšana
Apskata integrāļus
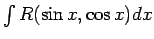 , kur
, kur 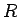 ir
racionāla savu argumentu funkcija.
ir
racionāla savu argumentu funkcija.
- Universālā trigonometriskā substitūcija
Integrāļus
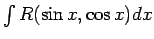 ar substitūciju
ar substitūciju
var reducēt uz integrāļiem no mainīgā 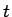 racionālām funkcijām.
racionālām funkcijām.
kur 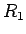 ir racionāla funkcija.
ir racionāla funkcija.
-
1.23. piemērs.
- Atrast
-
1.24. piemērs.
- Atrast
Šos divus integrāļus pievieno pamatintegrāļu tabulai.
-
1.11. piezīme.
- Universālā trigonometriskā substitūcija bieži
integrāļus
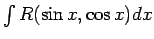 reducē uz samērā sarežģītu
racionālu funkciju integrēšanu. Tāpēc apskata citus paņēmienus šādu
integrāļu izskaitļošanai.
reducē uz samērā sarežģītu
racionālu funkciju integrēšanu. Tāpēc apskata citus paņēmienus šādu
integrāļu izskaitļošanai.
- Apskata gadījumus, kad
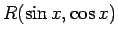 ir nepāra funkcija
attiecībā pret
ir nepāra funkcija
attiecībā pret 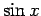 vai
vai 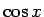 , t.i.,
vai
vai kad šī funkcija ir pāra funkcija attiecībā pret
, t.i.,
vai
vai kad šī funkcija ir pāra funkcija attiecībā pret 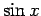 un
un 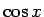 , t.i.,
, t.i.,
Šādos gadījumos lieto substitūciju atbilstoši
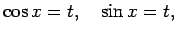
vai
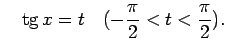
Piemēram, ja
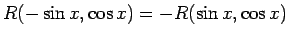 , tad
, tad
kur 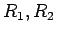 ir racionālas savu argumentu funkcijas. (Pārējos
gadījumus apskatīt patstāvīgi).
ir racionālas savu argumentu funkcijas. (Pārējos
gadījumus apskatīt patstāvīgi).
-
1.12. piezīme.
- Funkciju
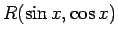 var izteikt kā šādu triju
veidu funkciju summu, t.i.,
var izteikt kā šādu triju
veidu funkciju summu, t.i.,
-
1.25. piemērs.
- Atrast
Šoreiz
un
-
1.26. piemērs.
- Atrast
Šoreiz
un
-
1.13. piezīme.
- Integrējot trigonometriskās funkcijas, izmanto dažādas
trigonometriskās formulas. Piemēram, reizinājumu pārveido
trigonometrisko funkciju summā, pazemina pakāpi, utt.
-
1.27. piemērs.
- Atrast
-
1.28. piemērs.
- Atrast
Tā kā
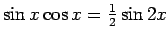 , tad
, tad
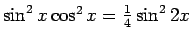 .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.8. Jautājumi
Augstāk: 1. NENOTEIKTAIS INTEGRĀLIS
Iepriekšējais: 1.6. Iracionālu funkciju integrēšana
2002-11-06
![]() , kur
, kur ![]() ir
racionāla savu argumentu funkcija.
ir
racionāla savu argumentu funkcija.
![]() ar substitūciju
ar substitūciju
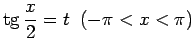
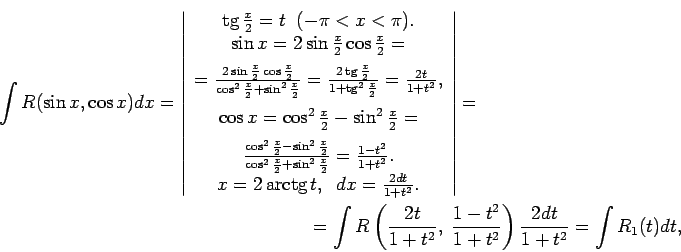
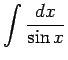
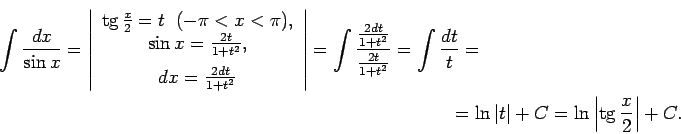
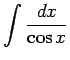
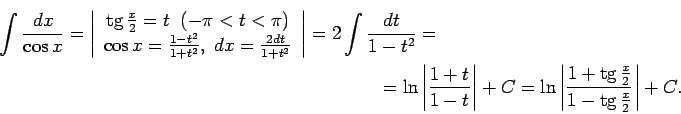
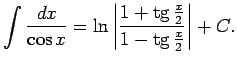
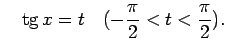
![]() , tad
, tad