Matemātika DU TSC
Nākamais: 1.9. Vingrinājumi Augstāk: 1.7. Trigonometrisko funkciju integrēšana Iepriekšējais: 1.7. Trigonometrisko funkciju integrēšana

1.8. Jautājumi

1. Formulēt integrālrēķinu pamatuzdevumu. Vai šis uzdevums ir atrisināms viennozīmīgi?
2. Definēt funkcijas $f$ primitīvo funkciju.
3. Definēt funkcijas $f$ nenoteikto integrāli.
4. Definēt funkcijas integrēšanas darbību.
5. Uzrakstīt pamatintegrāļu tabulu.
6. Formulēt nenoteiktā integrāļa pamatīpašības.
7. Nosaukt integrēšanas pamatmetodes nenoteiktajā integrālī.
8. Uzrakstīt parciālās integrēšanas formulu.
9. Nosaukt funkcijas, kuras integrē parciāli.
10. Uzrakstīt integrēšanas ar mainīgā aizvietošanu formulu.
11. Definēt elementārdaļas.
12. Definēt īstu un neīstu daļu $\frac{P(x)}{Q(x)}$.
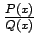13. Uzrakstīt īstas daļas sadalījumu elementārdaļu summā.
14. Paskaidrot, kā praktiski veic īstas daļas sadalījumu elementārdaļu summā.
15. Paskaidrot, kā integrē neīstu daļu.
16. Paskaidrot, kā integrē katru no elementārdaļām.
17. Paskaidrot, kā integrāļa 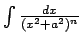$\int\frac{dx}{(x^2+a^2)^n}$ izskaitļošanā izmanto rekurences formulu.
18. Kāda ir iracionālu funkciju integrēšanas būtība?
19. Paskaidrot, kā integrē funkciju $R\left(x, \sqrt[n]{\frac{ax+b}{cx+d}}\right)$.
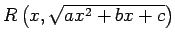20. Paskaidrot, kā integrē funkciju $R\left(x, \sqrt{ax^2+bx+c}\right)$ atkarībā no kvadrāttrinoma koeficientiem.
21. Paskaidrot, kā integrē binomiālo diferenciāli $x^m(a+bx^n)^pdx$.
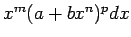22. Paskaidrot, kā ar universālo trigonometrisko substitūciju integrē funkciju $R(\sin x, \cos x)$.
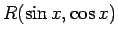23. Kādi ir citi paņēmieni funkciju 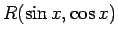$R(\sin x, \cos x)$ integrēšanā.

Matemātika DU TSC
Nākamais: 1.9. Vingrinājumi Augstāk: 1.7. Trigonometrisko funkciju integrēšana Iepriekšējais: 1.7. Trigonometrisko funkciju integrēšana