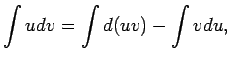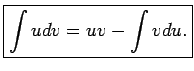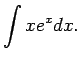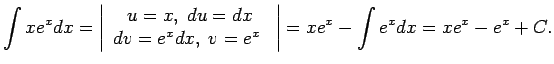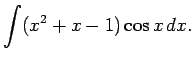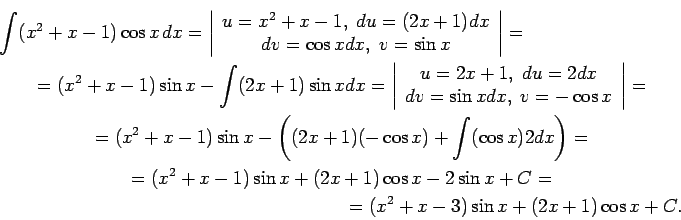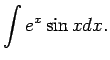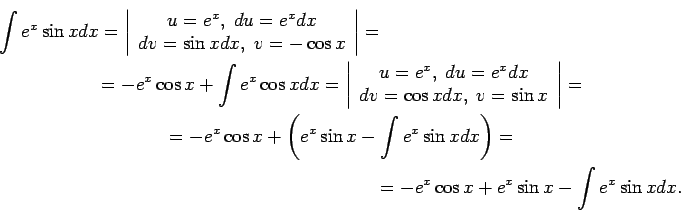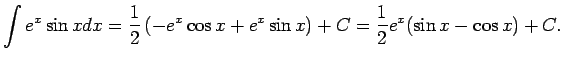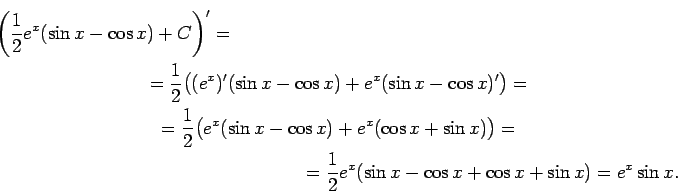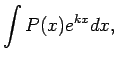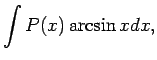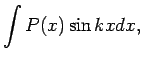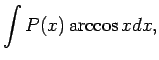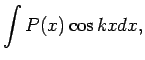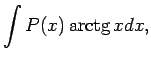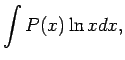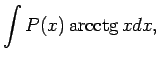Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.4.2. Integrēšana ar mainīgā aizvietošanu
Augstāk: 1.4. Integrēšanas pamatmetodes
Iepriekšējais: 1.4. Integrēšanas pamatmetodes
Apskata divas intervālā 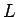 diferencējamas funkcijas
diferencējamas funkcijas 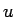 un
un 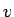 .
Atrod šo funkciju reizinājuma diferenciāli:
No šīs vienādības iegūst, ka
Integrē šo vienādību un izmanto nenoteiktā integrāļa īpašības:
.
Atrod šo funkciju reizinājuma diferenciāli:
No šīs vienādības iegūst, ka
Integrē šo vienādību un izmanto nenoteiktā integrāļa īpašības:
Iegūto formulu sauc par parciālās integrēšanas formulu nenoteiktajā
integrālī. (Integrēšanas konstanti neraksta, jo var uzskatīt, ka tā ietilpst otrajā
saskaitāmajā).
Funkcija 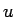 un diferenciālis
un diferenciālis 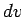 jāizvēlas tā, lai iegūtais
integrālis būtu tabulārs vai vismaz vienkāršāks par doto.
(Ja apzīmējumi nav izvēlēti pareizi,
tad iegūst sarežģītāku integrāli, nekā dotais.)
jāizvēlas tā, lai iegūtais
integrālis būtu tabulārs vai vismaz vienkāršāks par doto.
(Ja apzīmējumi nav izvēlēti pareizi,
tad iegūst sarežģītāku integrāli, nekā dotais.)
Atrodod integrāļus, apzīmējumus un palīgaprēķinus parasti ieslēdz
vertikālās svītrās.
-
1.4. piemērs.
- Atrast
-
1.2. piezīme.
- Parciālās integrēšanas formulu dažreiz nākas pielietot
atkārtoti.
-
1.5. piemērs.
- Atrast
-
1.3. piezīme.
- Atkārtoti pielietojot parciālās integrēšanas formulu,
dažreiz nonāk pie izteiksmes, kas satur doto integrāli. No iegūtās
vienādības izsaka doto integrāli.
-
1.6. piemērs.
- Atrast
Seko, ka
Lai pārbaudītu iegūto rezultātu, atvasina šīs vienādības labo pusi.
Integrālis atrasts pareizi.
-
1.4. piezīme.
- Parciālās integrēšanas formulu lieto, lai atrastu
šādus integrāļus:
kur 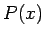 ir polinoms, bet
ir polinoms, bet 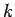 ir reāls skaitlis.
ir reāls skaitlis.
Pirmajos trijos piemēros apzīmē 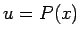 , bet pārējos - par
, bet pārējos - par 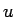 izvēlas funkciju, ar kuru reizināts polinoms.
izvēlas funkciju, ar kuru reizināts polinoms.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.4.2. Integrēšana ar mainīgā aizvietošanu
Augstāk: 1.4. Integrēšanas pamatmetodes
Iepriekšējais: 1.4. Integrēšanas pamatmetodes
2002-11-06