


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 6.4. Jautājumi
Augstāk: 6. NEĪSTIE INTEGRĀĻI
Iepriekšējais: 6.2. Pirmā veida neīstie integrāļi
Apskata integrāļus no intervālā ![$ [a;b]$](img524.gif) neierobežotām
funkcijām. Tādus integrāļus
neierobežotām
funkcijām. Tādus integrāļus
 sauc par
otrā veida neīstajiem integrāļiem.
sauc par
otrā veida neīstajiem integrāļiem.
Apskata intervālā 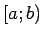 nepārtrauktu funkciju, kas ir
neierobežota punkta
nepārtrauktu funkciju, kas ir
neierobežota punkta 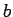 apkārtnē (6.2. zīm.).
apkārtnē (6.2. zīm.).
Jebkuram
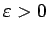 ir definēts noteiktais integrālis
ir definēts noteiktais integrālis
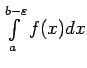 . Otrā veida neīsto integrāli
definē kā robežu no šī noteiktā integrāļa, kad
. Otrā veida neīsto integrāli
definē kā robežu no šī noteiktā integrāļa, kad
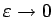 , t.i.,
, t.i.,
Ja eksistē galīga robeža, tad saka, ka neīstais integrālis
konverģē, šo robežu nosauc par neīstā integrāļa vērtību. Pretējā
gadījumā saka, ka neīstais integrālis diverģē.
Ja
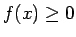 , tad šādu neīsto integrāli
, tad šādu neīsto integrāli
 var interpretēt ģeometriski kā bezgalīgi augstas līklīnijas
trapeces laukumu (6.2. zīm.).
var interpretēt ģeometriski kā bezgalīgi augstas līklīnijas
trapeces laukumu (6.2. zīm.).
Analogi apzīmē un definē neīsto integrāli, kad zemintegrāļa
funkcija nav ierobežota punkta 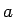 apkārtnē, proti,
apkārtnē, proti,
Ja zemintegrāļa funkcija ir neierobežota integrēšanas intervāla
![$ [a;b]$](img524.gif) iekšējā punktā
iekšējā punktā 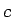 , tad šādu neīsto integrāli definē kā
divu iepriekš apskatīto integrāļu summu (6.3. zīm.),
t.i.,
, tad šādu neīsto integrāli definē kā
divu iepriekš apskatīto integrāļu summu (6.3. zīm.),
t.i.,
Pie tam integrāli
 sauc par
konverģentu, ja konverģē abi labās puses integrāļi.
sauc par
konverģentu, ja konverģē abi labās puses integrāļi.
-
6.3. piezīme.
- Otrā veida neīstajiem integrāļiem ir spēkā
salīdzināšanas teorēmas, kas ir analogas atbilstošajām
teorēmām par pirmā veida neīstajiem integrāļiem.
-
6.3. piemērs.
- Izpētīt uz konverģenci šādus neīstos integrāļus
- Funkcija
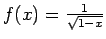 ir neierobežota
punkta
ir neierobežota
punkta 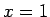 apkārtnē, tāpēc
apkārtnē, tāpēc
Otrā veida neīstais integrālis konverģē un tā skaitliskā
vērtība ir 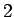 .
.
- Funkcija
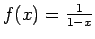 ir neierobežota
punkta
ir neierobežota
punkta 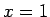 apkārtnē, tāpēc
apkārtnē, tāpēc
Neīstais integrālis diverģē.
- Funkcija
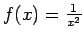 nav ierobežota punkta
nav ierobežota punkta
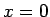 apkārtnē, tāpēc
Apskata atsevišķi katru labās puses integrāli.
Analogi
Abi neīstie integrāļi diverģē, diverģē arī dotais neīstais
integrālis (lai noskaidrotu tā diverģenci, ir pietiekami
noskaidrot tikai viena labās puses integrāļa diverģenci.)
apkārtnē, tāpēc
Apskata atsevišķi katru labās puses integrāli.
Analogi
Abi neīstie integrāļi diverģē, diverģē arī dotais neīstais
integrālis (lai noskaidrotu tā diverģenci, ir pietiekami
noskaidrot tikai viena labās puses integrāļa diverģenci.)
- Piezīme.
- Ja neievērotu, ka ir dots neīstais
integrālis, t.i., ka zemintegrāļa funkcija ir neierobežota
integrēšanas intervāla iekšējā punktā
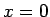 , un aprēķinus
veiktu pēc Ņūtona-Leibnica formulas:
tad, protams, pieļautu rupju kļūdu.
, un aprēķinus
veiktu pēc Ņūtona-Leibnica formulas:
tad, protams, pieļautu rupju kļūdu.
- Funkcija
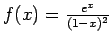 ir neierobežota
punkta
ir neierobežota
punkta 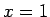 apkārtnē. Intervālā
apkārtnē. Intervālā
![$ [0;1-\varepsilon]$](img1304.gif) funkcija
ir nepārtraukta, tātad tai eksistē primitīvā funkcija, bet šo
primitīvo funkciju nevar izteikt caur galīga skaita
elementārajām funkcijām. Lai izpētītu šo integrāli uz
konverģenci, pielieto salīdzināšanas teorēmu. Visiem
funkcija
ir nepārtraukta, tātad tai eksistē primitīvā funkcija, bet šo
primitīvo funkciju nevar izteikt caur galīga skaita
elementārajām funkcijām. Lai izpētītu šo integrāli uz
konverģenci, pielieto salīdzināšanas teorēmu. Visiem 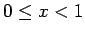 ir spēkā nevienādība
Pie tam neīstais integrālis
ir spēkā nevienādība
Pie tam neīstais integrālis
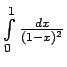 diverģē. Tādējādi diverģē
arī dotais neīstais integrālis.
diverģē. Tādējādi diverģē
arī dotais neīstais integrālis.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 6.4. Jautājumi
Augstāk: 6. NEĪSTIE INTEGRĀĻI
Iepriekšējais: 6.2. Pirmā veida neīstie integrāļi
2002-11-06
 sauc par
otrā veida neīstajiem integrāļiem.
sauc par
otrā veida neīstajiem integrāļiem.
![]() neierobežotām
funkcijām. Tādus integrāļus
neierobežotām
funkcijām. Tādus integrāļus
 sauc par
otrā veida neīstajiem integrāļiem.
sauc par
otrā veida neīstajiem integrāļiem.
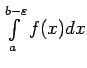 . Otrā veida neīsto integrāli
definē kā robežu no šī noteiktā integrāļa, kad
. Otrā veida neīsto integrāli
definē kā robežu no šī noteiktā integrāļa, kad
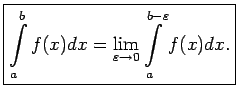
 var interpretēt ģeometriski kā bezgalīgi augstas līklīnijas
trapeces laukumu (6.2. zīm.).
var interpretēt ģeometriski kā bezgalīgi augstas līklīnijas
trapeces laukumu (6.2. zīm.).
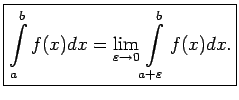
![]() iekšējā punktā
iekšējā punktā ![]() , tad šādu neīsto integrāli definē kā
divu iepriekš apskatīto integrāļu summu (6.3. zīm.),
t.i.,
, tad šādu neīsto integrāli definē kā
divu iepriekš apskatīto integrāļu summu (6.3. zīm.),
t.i.,
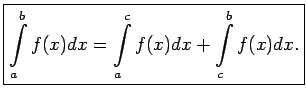
 sauc par
konverģentu, ja konverģē abi labās puses integrāļi.
sauc par
konverģentu, ja konverģē abi labās puses integrāļi.
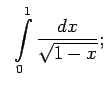
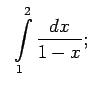
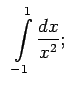
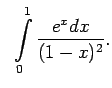
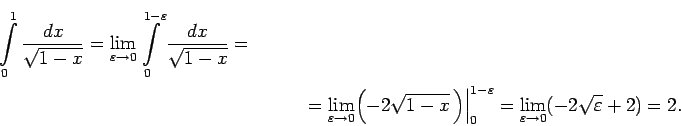
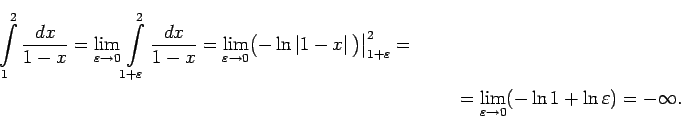
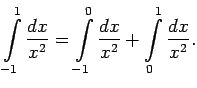
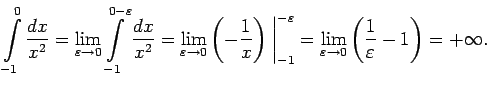
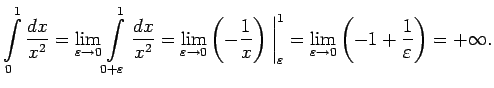
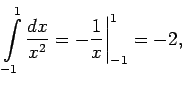
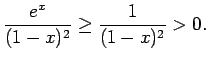
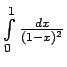 diverģē. Tādējādi diverģē
arī dotais neīstais integrālis.
diverģē. Tādējādi diverģē
arī dotais neīstais integrālis.