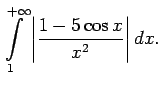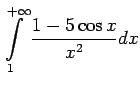Apskata bezgalīgā intervālā
 .
.
Apskata bezgalīgā intervālā
![]() nepārtrauktu funkciju
nepārtrauktu funkciju
![]() . Jebkurā galīgā intervālā šī funkcija ir integrējama un
tāpēc eksistē
. Jebkurā galīgā intervālā šī funkcija ir integrējama un
tāpēc eksistē
 .
.
Pirmā veida neīsto integrāli
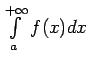 definē šādi:
definē šādi:
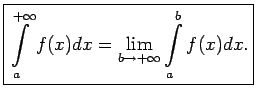
Ja eksistē galīga robeža, tad saka, ka neīstais integrālis konverģē un šo robežu nosauc par neīstā integrāļa vērtību. Pretējā gadījumā saka, ka neīstais integrālis diverģē.
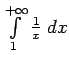 ,
,
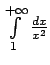 .
.
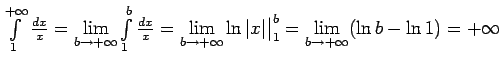 .
.
Neīstais integrālis diverģē.
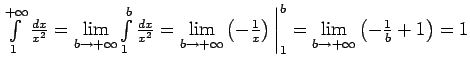 .
.
Neīstais integrālis konverģē un tā skaitliskā vērtība ir
Ģeometriski neīstā integrāļa
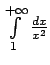 vērtību var interpretēt kā
bezgalīgas līklīnijas trapeces laukumu. Neīstajam integrālim
vērtību var interpretēt kā
bezgalīgas līklīnijas trapeces laukumu. Neīstajam integrālim
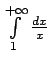 šādu ģeometrisko
interpretāciju sniegt nevar. Tas ir izskaidrojams ar to, ka līnija
šādu ģeometrisko
interpretāciju sniegt nevar. Tas ir izskaidrojams ar to, ka līnija
![]() ļoti strauji tuvojas abscisu asij, kad
ļoti strauji tuvojas abscisu asij, kad
![]() , bet otra līnija
, bet otra līnija
![]() tuvojas
tai daudz lēnāk, kaut gan abscisu ass ir asimptota arī šai līnijai
(6.1. zīm.).
tuvojas
tai daudz lēnāk, kaut gan abscisu ass ir asimptota arī šai līnijai
(6.1. zīm.).
Neīsto integrāli ar bezgalīgu apakšējo integrēšanas robežu definē līdzīgi:
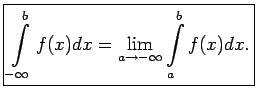
Neīsto integrāli, kuram abas integrēšanas robežas ir bezgalīgas, definē šādi:
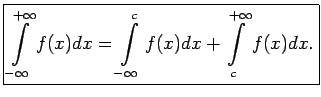
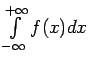 sauc par konverģentu tad un tikai tad, kad konverģē abi
neīstie integrāļi
sauc par konverģentu tad un tikai tad, kad konverģē abi
neīstie integrāļi
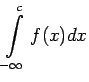 un
un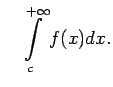
Neīsto integrāļu pētīšana nesagādā grūtības, ja zemintegrāļa
funkcijai ![]() var atrast primitīvo funkciju
var atrast primitīvo funkciju ![]() . Turpretī,
ja zemintegrāļa funkcijai primitīvo funkciju atrast neizdodas, tad
neīstos integrāļus pēta uz konverģenci, izmantojot
salīdzināšanas teorēmu.
. Turpretī,
ja zemintegrāļa funkcijai primitīvo funkciju atrast neizdodas, tad
neīstos integrāļus pēta uz konverģenci, izmantojot
salīdzināšanas teorēmu.
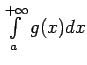 konverģē, tad
konverģē arī
konverģē, tad
konverģē arī
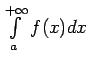 ;
;
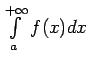 diverģē, tad
diverģē arī
diverģē, tad
diverģē arī
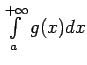 .
.
![]() 1. Tā kā neīstais integrālis
1. Tā kā neīstais integrālis
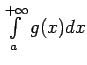 konverģē, tad eksistē galīga
robeža
konverģē, tad eksistē galīga
robeža
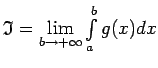 .
.
Visiem
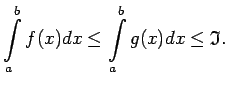
 ir integrēšanas augšējās
robežas
ir integrēšanas augšējās
robežas 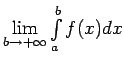 , kas nepārsniedz
, kas nepārsniedz
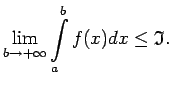
Tas nozīmē, ka neīstais integrālis
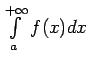 konverģē.
konverģē.
2. Tā kā neīstais integrālis
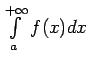 diverģē un
diverģē un
 ir integrēšanas augšējās
robežas
ir integrēšanas augšējās
robežas 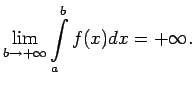
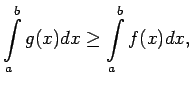
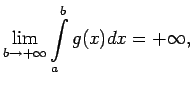
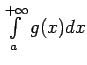 diverģē.
diverģē.
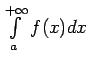 konverģences izriet
konverģences izriet
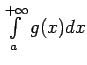 konverģence un no
konverģence un no
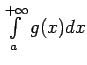 diverģences izriet
diverģences izriet
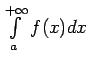 diverģence.
diverģence.
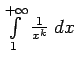 .
.
Viegli pamatot, ka šāds integrālis konverģē, ja
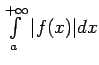 konverģē, tad konverģē arī
integrālis
konverģē, tad konverģē arī
integrālis
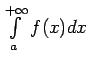 .
.
![]() Apskata divas palīgfunkcijas
Apskata divas palīgfunkcijas
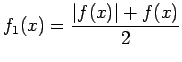 un
un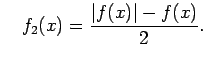
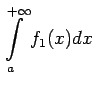 un
un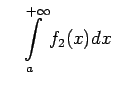
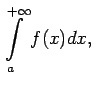
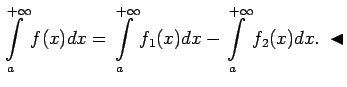
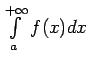 sauc par absolūti konverģentu, ja konverģē integrālis
sauc par absolūti konverģentu, ja konverģē integrālis
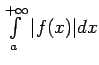 .
.
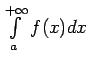 sauc par nosacīti
(neabsolūti) konverģentu, ja diverģē integrālis
sauc par nosacīti
(neabsolūti) konverģentu, ja diverģē integrālis
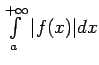 .
.
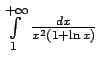 ,
,
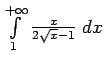 ,
,
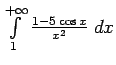 .
.
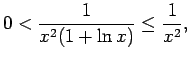
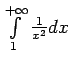 konverģē. Saskaņā ar
salīdzināšanas teorēmu konverģē integrālis
konverģē. Saskaņā ar
salīdzināšanas teorēmu konverģē integrālis
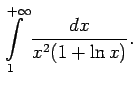
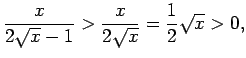
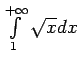 diverģē. Saskaņā ar
salīdzināšanas teorēmu diverģē integrālis
diverģē. Saskaņā ar
salīdzināšanas teorēmu diverģē integrālis
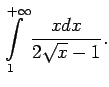
Visiem
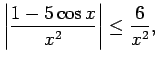
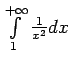 konverģē. Tāpēc
konverģē integrālis
konverģē. Tāpēc
konverģē integrālis