Matemātika DU TSC
Nākamais: 6.2. Pirmā veida neīstie integrāļi Augstāk: 6. NEĪSTIE INTEGRĀĻI Iepriekšējais: 6. NEĪSTIE INTEGRĀĻI

6.1. Neīstā integrāļa jēdziens

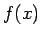Iepriekšējās tēmās tika apskatīti integrāļi $\int\limits_a^bf(x)dx$ pa galīgu integrēšanas intervālu $[a;b]$ no šajā intervālā ierobežotas funkcijas $f(x)$. Šādus noteiktos integrāļus mēdz saukt arī par īstajiem integrāļiem. Noteiktais integrālis zaudē jēgu, ja integrēšanas intervāls ir bezgalīgs vai zemintegrāļa funkcija integrēšanas intervālā nav ierobežota. Dažreiz noteiktā integrāļa jēdzienu var vispārināt arī uz šiem gadījumiem. Iegūtos integrāļus sauc par neīstajiem integrāļiem. Šādus integrāļus nevar definēt pēc analoģijas ar īstajiem integrāļiem, sastādot integrālsummas un pārejot pie robežas.

Izšķir triju veidu neīstos integrāļus.

6.1. definīcija. 

Par pirmā veida neīstajiem integrāļiem sauc tādus integrāļus, kuriem vismaz viena no integrēšanas robežām ir bezgalīga, bet zemintegrāļa funkcija ir ierobežota integrēšanas intervālā.

6.2. definīcija. 

Par otrā veida neīstajiem integrāļiem sauc tādus integrāļus, kuriem zemintegrāļa funkcija nav ierobežota integrēšanas intervālā $[a;b]$.

6.3. definīcija. 

Par trešā veida neīstajiem integrāļiem sauc tādus integrāļus, kuriem vismaz viena no integrēšanas robežām ir bezgalīga un zemintegrāļa funkcija nav ierobežota integrēšanas intervālā.

Matemātika DU TSC
Nākamais: 6.2. Pirmā veida neīstie integrāļi Augstāk: 6. NEĪSTIE INTEGRĀĻI Iepriekšējais: 6. NEĪSTIE INTEGRĀĻI