Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 5.2.1. Jautājumi
Augstāk: 5. PIELIKUMS
Iepriekšējais: 5.1.2. Vingrinājumi
Apskata divu argumentu funkciju 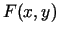 un vienādojumu
un vienādojumu
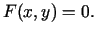 |
(5.1) |
Plaknes apakškopu 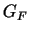 sauc par vienādojuma grafiku, ja
šīs kopas punkti apmierina vienādojumu (5.1). Apzīmē
ar
sauc par vienādojuma grafiku, ja
šīs kopas punkti apmierina vienādojumu (5.1). Apzīmē
ar 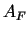 grafika
grafika 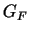 projekciju uz abscisu asi. Turpmāk apskata
tādus vienādojumus (5.1), kuru grafiks nav tukša kopa.
projekciju uz abscisu asi. Turpmāk apskata
tādus vienādojumus (5.1), kuru grafiks nav tukša kopa.
Piemēram, vienādojuma
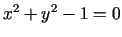 grafiks ir riņķa līnija, bet
vienādojuma
grafiks ir riņķa līnija, bet
vienādojuma
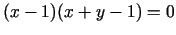 grafiks ir taisnes
grafiks ir taisnes 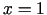 un
un
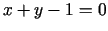 .
.
Ja vienādojuma (5.1) grafiks  savstarpēji
viennozīmīgi projicējas uz
savstarpēji
viennozīmīgi projicējas uz  , tad eksistē tāda vienīgā reālā
mainīgā
, tad eksistē tāda vienīgā reālā
mainīgā  funkcija
funkcija 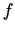 ar definīcijas apgabalu
ar definīcijas apgabalu 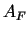 , kuras
grafiks sakrīt ar vienādojuma (5.1) grafiku. Funkcija
, kuras
grafiks sakrīt ar vienādojuma (5.1) grafiku. Funkcija
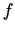 katram
katram 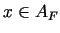 piekārto to vienīgo
piekārto to vienīgo 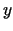 , kuram
, kuram 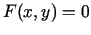 .
Tādos gadījumos saka, ka vienādojums (5.1) netieši
(apslēptā veidā) uzdod mainīgā
.
Tādos gadījumos saka, ka vienādojums (5.1) netieši
(apslēptā veidā) uzdod mainīgā  funkciju
funkciju 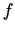 .
.
Bieži vienādojuma (5.1) grafiks 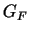 neprojicējas
viennozīmīgi uz
neprojicējas
viennozīmīgi uz 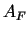 . Tādos gadījumos kopā
. Tādos gadījumos kopā 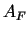 ir uzdotas
bezgalīgi daudzas
ir uzdotas
bezgalīgi daudzas  funkcijas, kuru grafiki sakrīt ar
vienādojuma (5.1) grafika
funkcijas, kuru grafiki sakrīt ar
vienādojuma (5.1) grafika 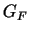 kaut kādu apakškopu.
Piemēram, ja intervālu
kaut kādu apakškopu.
Piemēram, ja intervālu ![$ [-1,1]$](img943.gif) sasmalcina ar starppunktiem
un katrā no intervāliem
sasmalcina ar starppunktiem
un katrā no intervāliem
![$ [x_{i-1},x_i]$](img945.gif) funkciju
funkciju  uzskata vienādu ar
uzskata vienādu ar
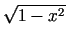 vai
vai
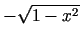 , tad iegūst funkcijas
, tad iegūst funkcijas 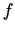 grafiku, kas ir
vienādojuma
grafika kaut kāda apakškopa, jo
grafiku, kas ir
vienādojuma
grafika kaut kāda apakškopa, jo
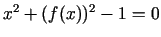 .
.
Pieņem, ka vienādojuma (5.1) grafiks 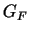 neprojicējas viennozīmīgi uz
neprojicējas viennozīmīgi uz 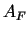 , bet eksistē tāds taisnstūris
ka grafika
, bet eksistē tāds taisnstūris
ka grafika 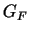 tā daļa, kas atrodas šajā taisnstūrī,
viennozīmīgi projicējas uz
tā daļa, kas atrodas šajā taisnstūrī,
viennozīmīgi projicējas uz ![$ [a,b]$](img951.gif) . Tad eksistē vienīgā reālā
mainīgā
. Tad eksistē vienīgā reālā
mainīgā  funkcija
funkcija 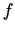 , kas uzdota intervālā
, kas uzdota intervālā ![$ [a,b]$](img951.gif) , kura
katram
, kura
katram
![$ x\in [a,b]$](img952.gif) piekārto tādu vienīgo
piekārto tādu vienīgo
![$ y\in [c,d]$](img953.gif) , ka
, ka
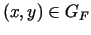 . Acīmredzami
. Acīmredzami
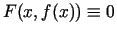 .
.
Saka, ka funkcija  netieši uzdota taisnstūrī
netieši uzdota taisnstūrī  ar
vienādojumu (5.1).
ar
vienādojumu (5.1).
Piemēram, vienādojums
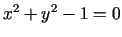 taisnstūrī
netieši uzdod funkciju
taisnstūrī
netieši uzdod funkciju
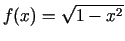 ,
bet taisnstūrī
uzdod
funkciju
,
bet taisnstūrī
uzdod
funkciju
 .
.
-
5.2. teorēma.
- (Netieši uzdotas funkcijas eksistence un
diferencējamība).
Ja funkcijai 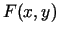 punkta
punkta 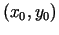 kaut kādā
apkārtnē eksistē nepārtraukti parciālie atvasinājumi
kaut kādā
apkārtnē eksistē nepārtraukti parciālie atvasinājumi
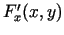 ,
, 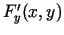 un
un
 ,
,
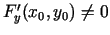 , tad eksistē tāds taisnstūris
kurā vienādojums
, tad eksistē tāds taisnstūris
kurā vienādojums 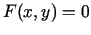 netieši uzdod argumenta
netieši uzdod argumenta  funkciju
funkciju  .
Funkcija
.
Funkcija 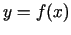 ir nepārtraukti diferencējama intervālā
ir nepārtraukti diferencējama intervālā
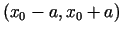 , pie tam
, pie tam
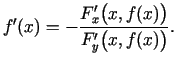 |
(5.2) |
 Vispirms pierāda netiešā veidā uzdotas
funkcijas eksistenci. No dotā seko, ka
Vispirms pierāda netiešā veidā uzdotas
funkcijas eksistenci. No dotā seko, ka
 vai
vai
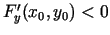 . Pieņem, piemēram, ka
. Pieņem, piemēram, ka
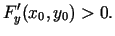 |
(5.3) |
Tā kā funkcija 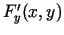 ir nepārtraukta punktā
ir nepārtraukta punktā 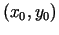 un
un
 , tad eksistē tāds taisnstūris (5.1. zīm.)
kurā
, tad eksistē tāds taisnstūris (5.1. zīm.)
kurā
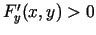 .
.
Apskata viena argumenta funkciju
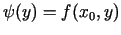 ,
,
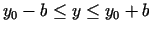 . Funkcija
. Funkcija 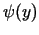 aug intervālā
aug intervālā
![$ [y_0-b, y_0+b]$](img978.gif) ,
jo
,
jo
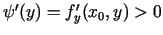 , pie tam
, pie tam
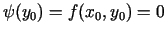 .
Tāpēc
.
Tāpēc
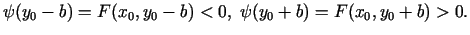 |
(5.4) |
Tā kā funkcija 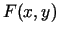 ir nepārtraukta, tad vienādības
(5.4) ir spēkā punktu
ir nepārtraukta, tad vienādības
(5.4) ir spēkā punktu
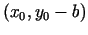 un
un
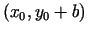 kaut
kādās apkārtnēs. Tāpēc eksistē tāds
kaut
kādās apkārtnēs. Tāpēc eksistē tāds
 , ka
visiem
, ka
visiem
![$ x\in [x_0-a,x_0+a]$](img985.gif) izpildās nevienādības
izpildās nevienādības
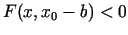 un un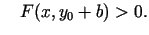 |
(5.5) |
Parāda, ka taisnstūrī
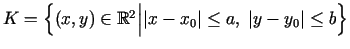 vienādojums
vienādojums 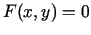 netieši uzdod
netieši uzdod  funkciju
funkciju
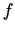 . Izvēlas patvaļīgu punktu
. Izvēlas patvaļīgu punktu
![$ x^{\ast}\in [x_0-a,\;x_0+a]$](img989.gif) un
apskata intervālā
un
apskata intervālā
![$ [y_0-b,\;y_0+b]$](img990.gif) nepārtrauktu viena argumenta
funkciju
nepārtrauktu viena argumenta
funkciju
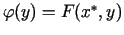 . Saskaņā ar nevienādībām
(5.5) funkcijai
. Saskaņā ar nevienādībām
(5.5) funkcijai
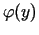 intervāla
intervāla
![$ [y_0-b, y_0+b]$](img978.gif) galapunktos vērtību zīmes ir pretējas, t.i.,
galapunktos vērtību zīmes ir pretējas, t.i.,
Saskaņā ar Bolcano teorēmu par nepārtrauktas funkcijas
starpvērtībām eksistē tāds
![$ y^{\ast}\in [y_0-b,y_0+b]$](img994.gif) , ka
, ka
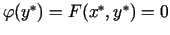 . Tā kā
. Tā kā
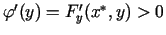 , tad funkcija
, tad funkcija
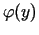 aug
intervālā
aug
intervālā
![$ [y_0-b, y_0+b]$](img978.gif) un vērtību nulle tā var iegūt tikai
vienā šī intervāla punktā.
un vērtību nulle tā var iegūt tikai
vienā šī intervāla punktā.
Tādējādi katram
![$ x\in [x_0-a,x_0+a]$](img985.gif) eksistē tāds vienīgais
eksistē tāds vienīgais
![$ y\in
[y_0-b,y_0+b]$](img997.gif) , ka
, ka 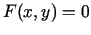 . Tas nozīmē, ka taisnstūrī
. Tas nozīmē, ka taisnstūrī 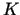 vienādojums
vienādojums 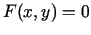 netieši uzdod
netieši uzdod  funkciju
funkciju 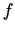 .
.
Tagad pierāda netiešā veidā uzdotas funkcijas diferencējamību.
Saskaņā ar Veierštrāsa 2. teorēmu slēgtā taisnstūrī 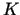 nepārtraukta
funkcija
nepārtraukta
funkcija 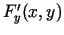 sasniedz šajā taisnstūrī savu vismazāko vērtību
sasniedz šajā taisnstūrī savu vismazāko vērtību
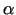 . Taisnstūrī
. Taisnstūrī 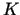
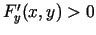 , tāpēc visiem
, tāpēc visiem
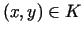 izpildās nevienādība
izpildās nevienādība
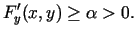 |
(5.6) |
Saskaņā ar Veierštrāsa 1. teorēmu taisnstūrī 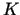 nepārtraukta
funkcija
nepārtraukta
funkcija 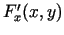 ir ierobežota šajā taisnstūrī. Tāpēc visiem
ir ierobežota šajā taisnstūrī. Tāpēc visiem
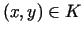 izpildās nevienādība
izpildās nevienādība
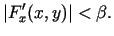 |
(5.7) |
Tātad funkcija 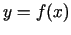 ir netieši uzdota taisnstūrī
ir netieši uzdota taisnstūrī 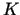 ar
vienādojumu
ar
vienādojumu 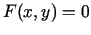 . Uz funkcijas
. Uz funkcijas  grafika
izvēlas divus punktus
grafika
izvēlas divus punktus  un
un
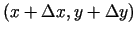 .
Skaidrs, ka
.
Skaidrs, ka 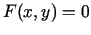 un
un
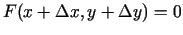 . Saskaņā ar
Lagranža formulu pārveido starpību
. Saskaņā ar
Lagranža formulu pārveido starpību
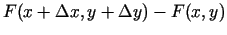 (acīmredzami šī starpība ir nulle). Iegūst, ka
(acīmredzami šī starpība ir nulle). Iegūst, ka
No šejienes
 |
(5.8) |
Ja izmanto nevienādības (5.6), (5.7), tad no
(5.8) iegūst, ka
 |
(5.9) |
Acīmredzami, ja
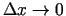 , tad arī
, tad arī
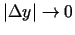 , tas nozīmē, ka netieši uzdotā funkcija
, tas nozīmē, ka netieši uzdotā funkcija  ir
nepārtraukta patvaļīgajā punktā
ir
nepārtraukta patvaļīgajā punktā
![$ x\in [x_0-a,x_0+a]$](img985.gif) . Ja vienādību
(5.8) izdala ar
. Ja vienādību
(5.8) izdala ar 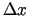 , izmanto parciālo
atvasinājumu nepārtrauktību un pāriet pie robežas, kad
, izmanto parciālo
atvasinājumu nepārtrauktību un pāriet pie robežas, kad
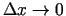 , tad iegūst, ka eksistē
, tad iegūst, ka eksistē
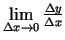 , kas vienāda ar
, kas vienāda ar
 . Tādējādi
. Tādējādi
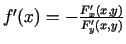 , kur
, kur 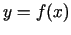 . No šīs
vienādības seko, ka atvasinājums
. No šīs
vienādības seko, ka atvasinājums  ne tikai eksistē
intervālā
ne tikai eksistē
intervālā
![$ [x_0-a,x_0+a]$](img1012.gif) , bet arī ir nepārtraukts šajā
intervālā, kā nepārtrauktu funkciju
dalījums.
, bet arī ir nepārtraukts šajā
intervālā, kā nepārtrauktu funkciju
dalījums.
-
5.3. piezīme.
- Ja vienādojums
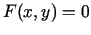 taisnstūrī
netieši uzdot funkciju
taisnstūrī
netieši uzdot funkciju  , tad formulu (5.2) var iegūt
formāli atvasinot pēc
, tad formulu (5.2) var iegūt
formāli atvasinot pēc  identitāti
identitāti
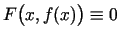 .
.
-
5.2. definīcija.
- Par kopu
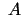 un
un 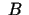 tiešo
jeb Dekarta reizinājumu
tiešo
jeb Dekarta reizinājumu
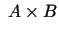 sauc tādu pāru
sauc tādu pāru
 kopu, kur
kopu, kur  un
un 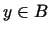 .
.
Piemēram, Dekarta reizinājumu
![$ [a,b]\times [c,d]$](img1020.gif) veido tādu reālu
skaitļu
veido tādu reālu
skaitļu  un
un 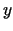 pāri
pāri  , kur
, kur
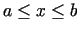 ,
,
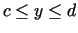 . Tika iegūts slēgts taisnstūris telpā
. Tika iegūts slēgts taisnstūris telpā
 .
.
-
5.3. definīcija.
- Par punkta
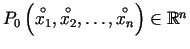 kubveida apkārtni
kubveida apkārtni
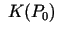 sauc telpas
sauc telpas
 tādu punktu
tādu punktu
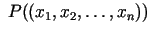 kopu, kur
kopu, kur
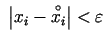 (i=1,...,n).
(i=1,...,n).
Acīmredzami, ja  ,
, 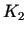 ir atbilstoši punktu
ir atbilstoši punktu
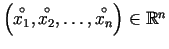 un
un
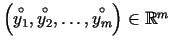 kubveida apkārtnes, tad
kubveida apkārtnes, tad
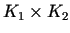 ir punkta
ir punkta
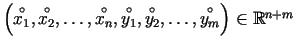 kubveida apkārtne. Apskata
kubveida apkārtne. Apskata  vienādojumu sistēmu ar
vienādojumu sistēmu ar 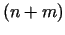 nezināmiem:
nezināmiem:
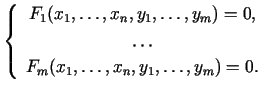 |
(5.10) |
Uzskata, ka funkcijas 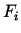
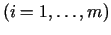 definētas punkta
definētas punkta
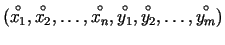 kaut kādā kubveida apkārtnē.
kaut kādā kubveida apkārtnē.
-
5.4. definīcija.
- Ja
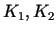 ir atbilstoši punktu
ir atbilstoši punktu
 ,
,
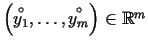 kubveida apkārtnes
un jebkuram punktam
kubveida apkārtnes
un jebkuram punktam
 eksistē tāds
vienīgais punkts
eksistē tāds
vienīgais punkts
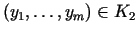 , ka
tad saka, ka kubveida apkārtnē
, ka
tad saka, ka kubveida apkārtnē
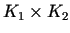 šī sistēma
netieši definē
šī sistēma
netieši definē
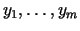 kā mainīgo
kā mainīgo
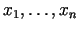 funkcijas.
funkcijas.
-
5.3. teorēma.
- Ja izpildās šādi nosacījumi:
- funkcijas
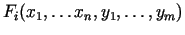
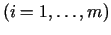 ir nepārtraukti diferencējamas punkta
ir nepārtraukti diferencējamas punkta
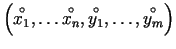 kubveida
apkārtnē,
kubveida
apkārtnē,
-
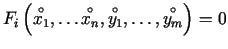
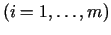 ,
,
- punktā
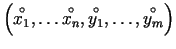 determinante
determinante
tad eksistē punktu
 un
un
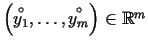 tādas kubveida apkārtnes
tādas kubveida apkārtnes  un
un 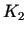 , ka kubveida apkārtnē
, ka kubveida apkārtnē
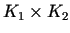 sistēma
(5.10)
netieši definē
sistēma
(5.10)
netieši definē
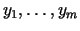 kā mainīgo
kā mainīgo
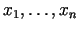 funkcijas.
Funkcijas
funkcijas.
Funkcijas
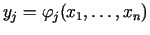 ir nepārtraukti diferencējamas
kubveida apkārtnē
ir nepārtraukti diferencējamas
kubveida apkārtnē  un
un
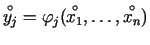
 .
.
-
5.4. piezīme.
- Šo teorēmu var pierādīt, piemēram, ar matemātiskās
indukcijas metodi.
-
5.2. piemērs.
- Noskaidrot, vai vienādojums
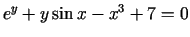 netieši uzdod diferencējamu funkciju.
netieši uzdod diferencējamu funkciju.
Funkcija
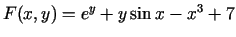 definēta visā
definēta visā 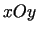 plaknē.
Visā plaknē eksistē nepārtraukti parciālie atvasinājumi
plaknē.
Visā plaknē eksistē nepārtraukti parciālie atvasinājumi
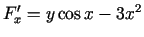 un
un
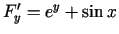 . Piemēram, punktā
. Piemēram, punktā 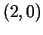 funkcijas
funkcijas
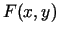 vērtība ir nulle, t.i.,
vērtība ir nulle, t.i.,  , bet parciālais
atvasinājums
(starp citu arī
, bet parciālais
atvasinājums
(starp citu arī
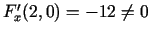 ). Saskaņā ar 5.2. teorēmu dotais vienādojums punkta
). Saskaņā ar 5.2. teorēmu dotais vienādojums punkta
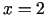 kaut kādā apkārtnē netieši definē
kaut kādā apkārtnē netieši definē 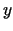 kā
kā  funkciju. (Šis vienādojums
punkta
funkciju. (Šis vienādojums
punkta 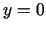 kaut kādā apkārtnē netieši definē
kaut kādā apkārtnē netieši definē  kā
kā 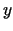 funkciju). No vienādojuma nav iespējams caur galīga skaita
elementārām funkcijām izteikt
funkciju). No vienādojuma nav iespējams caur galīga skaita
elementārām funkcijām izteikt 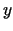 caur
caur  (nevar izteikt arī
(nevar izteikt arī  caur
caur
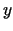 ). Atrod, piemēram,
). Atrod, piemēram, 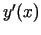 . Tam nolūkam izmanto formulu
. Tam nolūkam izmanto formulu
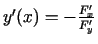 . Tādējādi
Atvasinājumu var atrast arī neizmantojot minēto formulu, bet
diferencējot pēc
. Tādējādi
Atvasinājumu var atrast arī neizmantojot minēto formulu, bet
diferencējot pēc  vienādojumu
vienādojumu
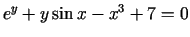 . Uz mainīgo
. Uz mainīgo
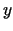 skatās kā uz
skatās kā uz  funkciju. Iegūst
funkciju. Iegūst
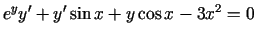 . Izsaka
. Izsaka
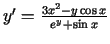 .
.
-
5.3. piemērs.
- Parādīt, ka vienādojumu sistēma
punkta
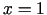 kaut kādā apkārtnē netieši uzdod
kaut kādā apkārtnē netieši uzdod 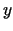 un
un 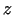 kā
kā  diferencējamas funkcijas. Izskaitļot
diferencējamas funkcijas. Izskaitļot 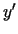 un
un 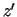 punktā
punktā 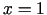 , ja
, ja
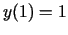 un
un 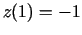 .
.
Funkcijas
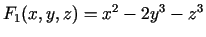 un
un
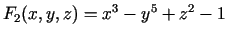 definētas patvaļīgām
definētas patvaļīgām 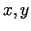 un
un 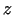 vērtībām. Parciālie atvasinājumi
vērtībām. Parciālie atvasinājumi
ir nepārtraukti patvaļīgām 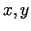 un
un 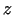 vērtībām. Punktā
vērtībām. Punktā 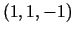 funkciju
funkciju
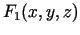 un
un
 vērtības ir nulle, t.i.,
bet atbilstošā funkcionāldeterminante
(skat.5.3. teorēmu) nav nulle. Tiešām
un punktā
vērtības ir nulle, t.i.,
bet atbilstošā funkcionāldeterminante
(skat.5.3. teorēmu) nav nulle. Tiešām
un punktā 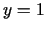 ,
, 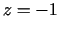 tās vērtība
tās vērtība
Saskaņā ar 5.3. teorēmu dotā vienādojumu sistēma punkta
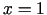 kaut kādā apkārtnē netieši uzdod
kaut kādā apkārtnē netieši uzdod 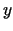 un
un 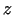 kā
kā  diferencējamas funkcijas. Lai izskaitļotu šo funkciju atvasinājumu
vērtības punktā
diferencējamas funkcijas. Lai izskaitļotu šo funkciju atvasinājumu
vērtības punktā 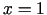 , vispirms diferencē pēc
, vispirms diferencē pēc  sistēmas abus
vienādojumus
sistēmas abus
vienādojumus
Tagad ievieto 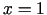 ,
, 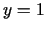 un
un 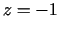 . Iegūst sistēmu
kuras atrisinājums ir
. Iegūst sistēmu
kuras atrisinājums ir
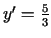 ,
,
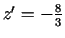 .
.
-
5.4. piemērs.
- Noskaidrot, vai vienādojums
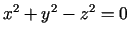 kaut kāda
punkta apkārtnē netieši uzdod, piemēram,
kaut kāda
punkta apkārtnē netieši uzdod, piemēram, 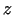 kā
kā  un
un 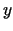 diferencējamu funkciju.
diferencējamu funkciju.
Funkcija
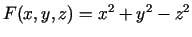 definēta patvaļīgām
definēta patvaļīgām 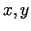 un
un 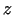 vērtībām. Parciālie atvasinājumi
vērtībām. Parciālie atvasinājumi 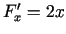 ,
, 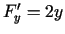 ,
, 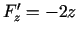 nepārtraukti jebkurā punktā
nepārtraukti jebkurā punktā 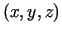 . Piemēram, punktā
. Piemēram, punktā
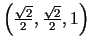 funkcijas
funkcijas 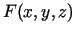 vērtība ir nulle,
t.i.,
vērtība ir nulle,
t.i.,
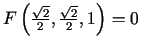 , bet parciālais atvasinājums
, bet parciālais atvasinājums
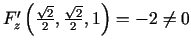 . Tāpēc punkta
. Tāpēc punkta
 ,
,
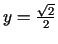 kaut kādā apkārtnē
dotais vienādojums netieši uzdod
kaut kādā apkārtnē
dotais vienādojums netieši uzdod 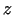 kā argumentu
kā argumentu  un
un 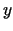 diferencējamu funkciju. Funkcijas
diferencējamu funkciju. Funkcijas 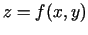 parciālos
atvasinājumus var atrast pēc formulām:
parciālos
atvasinājumus var atrast pēc formulām:
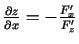 ,
,
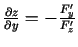 . Tādējādi
. Tādējādi
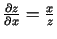 ,
,
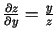 . Parciālos atvasinājumus
. Parciālos atvasinājumus
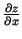 un
un
 var atrast, diferencējot vienādojumu
var atrast, diferencējot vienādojumu
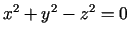 vienreiz
pēc
vienreiz
pēc  un otrreiz pēc
un otrreiz pēc 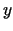 . Iegūst vienādojumu sistēmu
Tās atrisinājums ir
. Iegūst vienādojumu sistēmu
Tās atrisinājums ir
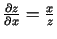 ,
,
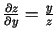 .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 5.2.1. Jautājumi
Augstāk: 5. PIELIKUMS
Iepriekšējais: 5.1.2. Vingrinājumi
2002-06-21
![]() un vienādojumu
un vienādojumu
![]() Vispirms pierāda netiešā veidā uzdotas
funkcijas eksistenci. No dotā seko, ka
Vispirms pierāda netiešā veidā uzdotas
funkcijas eksistenci. No dotā seko, ka
![]() vai
vai
![]() . Pieņem, piemēram, ka
. Pieņem, piemēram, ka
![]() vienādojums
vienādojums ![]() netieši uzdod
netieši uzdod ![]() funkciju
funkciju
![]() . Izvēlas patvaļīgu punktu
. Izvēlas patvaļīgu punktu
![]() un
apskata intervālā
un
apskata intervālā
![]() nepārtrauktu viena argumenta
funkciju
nepārtrauktu viena argumenta
funkciju
![]() . Saskaņā ar nevienādībām
(5.5) funkcijai
. Saskaņā ar nevienādībām
(5.5) funkcijai
![]() intervāla
intervāla
![]() galapunktos vērtību zīmes ir pretējas, t.i.,
galapunktos vērtību zīmes ir pretējas, t.i.,
![]() , ka
, ka
![]() . Tā kā
. Tā kā
![]() , tad funkcija
, tad funkcija
![]() aug
intervālā
aug
intervālā
![]() un vērtību nulle tā var iegūt tikai
vienā šī intervāla punktā.
un vērtību nulle tā var iegūt tikai
vienā šī intervāla punktā.
![]() nepārtraukta
funkcija
nepārtraukta
funkcija ![]() ir ierobežota šajā taisnstūrī. Tāpēc visiem
ir ierobežota šajā taisnstūrī. Tāpēc visiem
![]() izpildās nevienādība
izpildās nevienādība
![]() ir netieši uzdota taisnstūrī
ir netieši uzdota taisnstūrī ![]() ar
vienādojumu
ar
vienādojumu ![]() . Uz funkcijas
. Uz funkcijas ![]() grafika
izvēlas divus punktus
grafika
izvēlas divus punktus ![]() un
un
![]() .
Skaidrs, ka
.
Skaidrs, ka ![]() un
un
![]() . Saskaņā ar
Lagranža formulu pārveido starpību
. Saskaņā ar
Lagranža formulu pārveido starpību
![]() (acīmredzami šī starpība ir nulle). Iegūst, ka
(acīmredzami šī starpība ir nulle). Iegūst, ka
![]() veido tādu reālu
skaitļu
veido tādu reālu
skaitļu ![]() un
un ![]() pāri
pāri ![]() , kur
, kur
![]() ,
,
![]() . Tika iegūts slēgts taisnstūris telpā
. Tika iegūts slēgts taisnstūris telpā
![]() .
.
![]() ,
, ![]() ir atbilstoši punktu
ir atbilstoši punktu
![]() un
un
![]() kubveida apkārtnes, tad
kubveida apkārtnes, tad
![]() ir punkta
ir punkta
![]() kubveida apkārtne. Apskata
kubveida apkārtne. Apskata ![]() vienādojumu sistēmu ar
vienādojumu sistēmu ar ![]() nezināmiem:
nezināmiem:
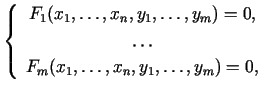
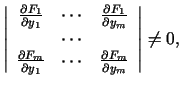

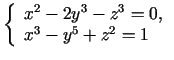
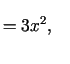
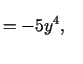
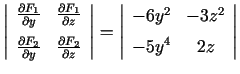
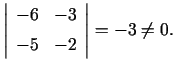
![]() kaut kādā apkārtnē netieši uzdod
kaut kādā apkārtnē netieši uzdod ![]() un
un ![]() kā
kā ![]() diferencējamas funkcijas. Lai izskaitļotu šo funkciju atvasinājumu
vērtības punktā
diferencējamas funkcijas. Lai izskaitļotu šo funkciju atvasinājumu
vērtības punktā ![]() , vispirms diferencē pēc
, vispirms diferencē pēc ![]() sistēmas abus
vienādojumus
sistēmas abus
vienādojumus