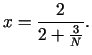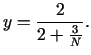Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3. LINEĀRĀS PROGRAMMĒŠANAS UZDEVUMI
Augstāk: 2.3. Minimuma punkta meklēšanas metodes vairāku
Iepriekšējais: 2.3.2. Šķēlumu metode
Soda funkciju metodes (saīsināti S.F.M.) pamatā ir ideja par
funkcijas  nosacītās minimizēšanas uzdevuma aizvietošanu ar
brīvās minimizēšanas uzdevumu virkni
nosacītās minimizēšanas uzdevuma aizvietošanu ar
brīvās minimizēšanas uzdevumu virkni
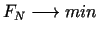 .
.
-
2.11. piemērs.
- Apskatīsim nosacītās minimizēšanas problēmu:
Izmantojot Lagranža metodi (skat. 1.2.4. apakšparagrāfu),
var iegūt šīs problēmas atrisinājumu:
Pielietosim S.F.M. Sastādīsim jaunu funkciju
kura ir atkarīga no parametra 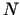 . Locekli
. Locekli
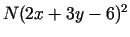 sauc
par sodu par nosacījuma neizpildīšanos: jo tālāk punkts
sauc
par sodu par nosacījuma neizpildīšanos: jo tālāk punkts
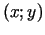 ir no taisnes
ir no taisnes
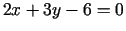 , jo lielāks ir elements
, jo lielāks ir elements
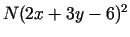 .
.
Meklējam problēmas
atrisinājumu, lietojot jebkuru brīva ekstrēma meklēšanas metodi.
Risinot sistēmu
atrodam
no kurienes seko, ka
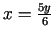 . Ievietojot
. Ievietojot  pēdējās
vienādojumu sistēmas otrajā vienādojumā, iegūsim
pēdējās
vienādojumu sistēmas otrajā vienādojumā, iegūsim
Tad
Kad 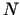 tiecas uz bezgalību, tad
tiecas uz bezgalību, tad
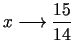 un un 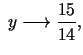 |
|
t.i.,  un
un 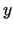 tiecas uz sākotnējā uzdevuma atrisinājumu.
tiecas uz sākotnējā uzdevuma atrisinājumu.
S.F.M. apraksts. Problēma:
Nosacījumi 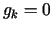 definē pieļaujamo apgabalu
definē pieļaujamo apgabalu 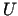 . Par
soda funkciju sauc funkciju
. Par
soda funkciju sauc funkciju 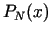 ar šādām
īpašībām:
ar šādām
īpašībām:
1)
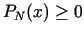 ,
, 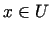 ,
,
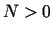 ;
;
2)
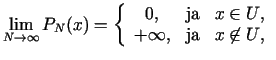
Iespējamās soda funkcijas:
Nobeigumā apskatīsim vēl vienu piemēru.
-
2.12. piemērs.
-
Soda funkcija:
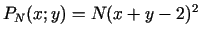 . Meklējam problēmas
. Meklējam problēmas
atrisinājumu. Risinot sistēmu
atrodam, ka
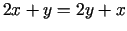 jeb
jeb 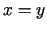 . Tāpēc no pirmā
vienādojuma izriet, ka
. Tāpēc no pirmā
vienādojuma izriet, ka
Tad
Acīmredzams, ja
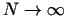 , tad
, tad
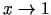 un
un
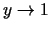 . Problēmas atrisinājums - punkts
. Problēmas atrisinājums - punkts 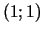 ,
kurā funkcija
,
kurā funkcija  iegūst nosacītu minimumu.
iegūst nosacītu minimumu.
-
2.5. piezīme.
- Izvērstāku informāciju par soda funkciju metodi
var atrast grāmatās [1], [3], [5].



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3. LINEĀRĀS PROGRAMMĒŠANAS UZDEVUMI
Augstāk: 2.3. Minimuma punkta meklēšanas metodes vairāku
Iepriekšējais: 2.3.2. Šķēlumu metode
2002-05-04
![]() nosacītās minimizēšanas uzdevuma aizvietošanu ar
brīvās minimizēšanas uzdevumu virkni
nosacītās minimizēšanas uzdevuma aizvietošanu ar
brīvās minimizēšanas uzdevumu virkni
![]() .
.
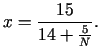
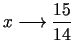 un
un 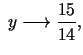
![]() ,
, ![]() ,
,
![]() ;
;
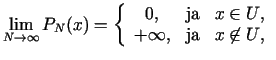
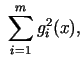
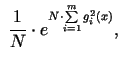
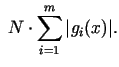
![]() . Meklējam problēmas
. Meklējam problēmas