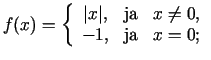Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.2. Minimuma punkta meklēšanas metodes
Augstāk: 2. SKAITLISKĀS METODES
Iepriekšējais: 2. SKAITLISKĀS METODES
Nepārtrauktas funkcijas jēdziens ir zināms no matemātiskās
analīzes kursa. Nepārtrauktas funkcijas grafiks ir
nepārtraukta līnija viena argumenta funkcijas gadījumā vai
nepārtraukta virsma (hipervirsma) divu un vairāku argumentu
funkcijas gadījumā. Pārtrauktas funkcijas grafikam var
būt pārtraukumi vai lēcieni. Diskrētu funkciju var uzdot ar savu
vērtību tabulu pie atsevišķām argumenta
vērtībām.
Negludo (nediferencējamo) funkciju
ekstrēmu punktu meklēšanas metodes var ilustrēt ar unimodālo
funkciju piemēru. Par unimodālām sauc viena argumenta
funkcijas, kurām definīcijas intervālā 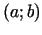 ir tikai
viens ekstrēma punkts (noteiktības labad pieņemsim, ka tas ir
minimums). Unimodālās funkcijas var būt arī
pārtrauktas.
ir tikai
viens ekstrēma punkts (noteiktības labad pieņemsim, ka tas ir
minimums). Unimodālās funkcijas var būt arī
pārtrauktas.
Apskatīsim unimodālo funkciju
piemērus.
-
2.1. piemērs.
- Nepārtrauktu unimodālu funkciju piemēri:
Funkcija 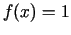 nav unimodāla nevienā intervālā, jo tai
jebkurā intervālā ir vairāki ekstrēma punkti.
nav unimodāla nevienā intervālā, jo tai
jebkurā intervālā ir vairāki ekstrēma punkti.
-
2.2. piemērs.
- Pārtraukto unimodālo funkciju piemēri:
kur
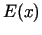 ir lielākais veselais skaitlis, kas nepārsniedz
ir lielākais veselais skaitlis, kas nepārsniedz  (t.i.,
(t.i., 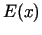 ir reālā skaitļa
ir reālā skaitļa  veselā daļa, kuru apzīmē arī ar
veselā daļa, kuru apzīmē arī ar
![$ [x]$](img450.gif) ).
).
No unimodālas funkcijas īpašībām izriet šāds
- Apgalvojums.
- Ja
 ir unimodāla funkcija un ja kādiem
ir unimodāla funkcija un ja kādiem
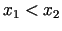 ir spēkā
ir spēkā
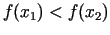 , tad minimuma punkts
, tad minimuma punkts
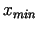 apmierina nosacījumu
apmierina nosacījumu
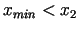 . Savukārt,
ja kādiem
. Savukārt,
ja kādiem
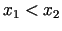 ir spēkā
ir spēkā
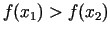 , tad
minimuma punkts
, tad
minimuma punkts 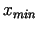 apmierina nosacījumu
apmierina nosacījumu
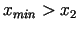 .
.
Šis apgalvojums ir dažu minimuma punktu meklēšanas
stratēģiju pamatā.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.2. Minimuma punkta meklēšanas metodes
Augstāk: 2. SKAITLISKĀS METODES
Iepriekšējais: 2. SKAITLISKĀS METODES
2002-05-04