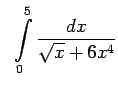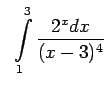Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: LITERATŪRA
Augstāk: 6.3. Otrā veida neīstie integrāļi
Iepriekšējais: 6.5. Vingrinājumi
- Izmantojot definīciju, izpētīt uz konverģenci šādus
neīstos integrāļus
- Izmantojot salīdzināšanas teorēmas, izpētīt uz
konverģenci šādus neīstos integrāļus



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: LITERATŪRA
Augstāk: 6.3. Otrā veida neīstie integrāļi
Iepriekšējais: 6.5. Vingrinājumi
2002-11-06
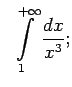
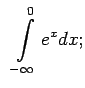
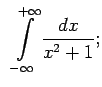
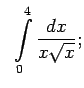
![$\displaystyle \;\;\int\limits_0^9\frac{dx}{\sqrt[3]{(x-1)^2}}.$](img1314.gif)
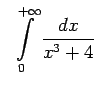
![$\displaystyle \;\;\int\limits_1^{+\infty}\frac{dx}{x^2+\sqrt[4]{x}}$](img1316.gif)
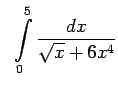
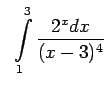
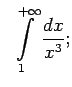
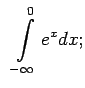
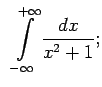
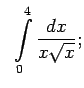
![$\displaystyle \;\;\int\limits_0^9\frac{dx}{\sqrt[3]{(x-1)^2}}.$](img1314.gif)
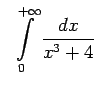
![$\displaystyle \;\;\int\limits_1^{+\infty}\frac{dx}{x^2+\sqrt[4]{x}}$](img1316.gif)