


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 6. NEĪSTIE INTEGRĀĻI
Augstāk: 5.6. Homogēnas plaknes figūras statisko momentu
Iepriekšējais: 5.8. Vingrinājumi
- Aprēķināt laukumu figūrai, kuru ierobežo šādas līknes:
-
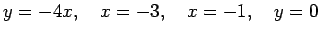 ;
;
-
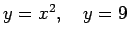 ;
;
-
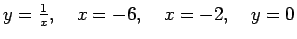 ;
;
-
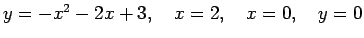 ;
;
-
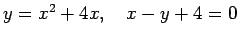 ;
;
- cikloīdas
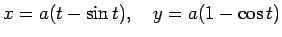 viena
arka un abscisu ass;
viena
arka un abscisu ass;
- astroīda
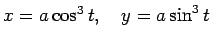 ;
;
- kardioīda
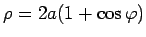 ;
;
- trīslapu roze
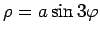 .
.
- Aprēķināt šādu līkņu garumus:
- ķēdes līnijai
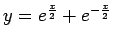 starp punktiem
starp punktiem 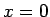 un
un 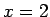 ;
;
-
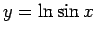 starp punktiem
starp punktiem
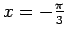 un
un
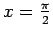 ;
;
- astroīdai
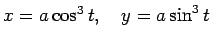 ;
;
- līknei
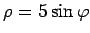 .
.
- Aprēķināt tilpumu ķermenim, kas rodas, rotējot ap
abscisu asi līklīnijas trapecei, kuru ierobežo šādas līknes:
-
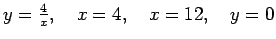 ;
;
-
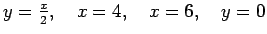 .
.
- Aprēķināt masas centru astroīdas
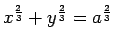 lokam, kas
atrodas 1. kvadrantā.
lokam, kas
atrodas 1. kvadrantā.
- Aprēķināt masas centru ķēdes līnijas
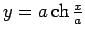 lokam starp punktiem
lokam starp punktiem
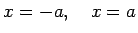 .
.
- Aprēķināt masas centru homogēnam trijstūrim, kuru
ierobežo taisnes
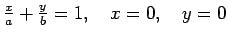 .
.
- Aprēķināt masas centru homogēnai figūrai, kuru ierobežo
līknes
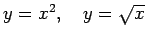 .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 6. NEĪSTIE INTEGRĀĻI
Augstāk: 5.6. Homogēnas plaknes figūras statisko momentu
Iepriekšējais: 5.8. Vingrinājumi
2002-11-06
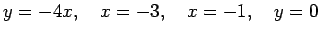 ;
;
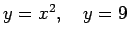 ;
;
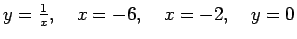 ;
;
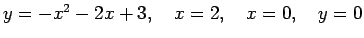 ;
;
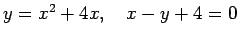 ;
;
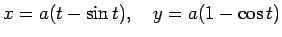 viena
arka un abscisu ass;
viena
arka un abscisu ass;
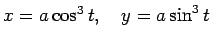 ;
;
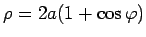 ;
;
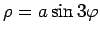 .
.
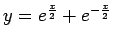 starp punktiem
starp punktiem 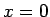 un
un 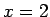 ;
;
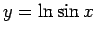 starp punktiem
starp punktiem
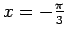 un
un
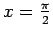 ;
;
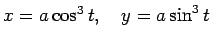 ;
;
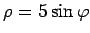 .
.
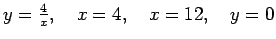 ;
;
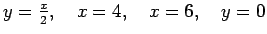 .
.