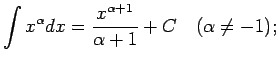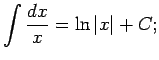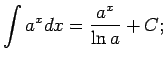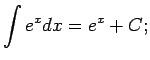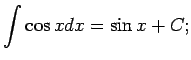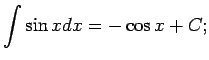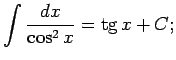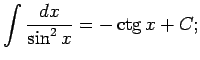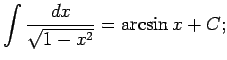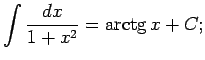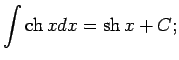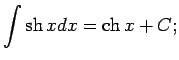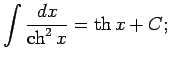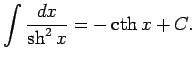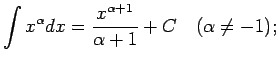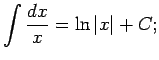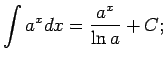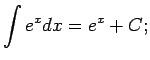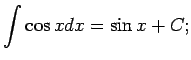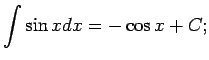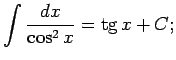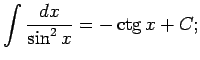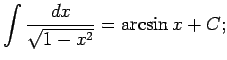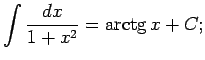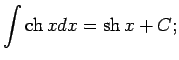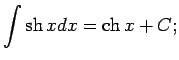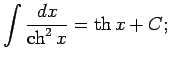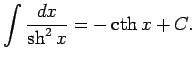Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.3. Nenoteiktā integrāļa pamatīpašības
Augstāk: 1. NENOTEIKTAIS INTEGRĀLIS
Iepriekšējais: 1.1. Primitīvā funkcija un nenoteiktais integrālis
No elementāro pamatfunkciju atvasinājumu tabulas un nenoteiktā
integrāļa definīcijas izriet šāda pamatintegrāļu
tabula.
Šo formulu pareizību var pārbaudīt tieši - atvasinot formulu labās
puses; rezultātā ir jāiegūst atbilstošā zemintegrāļa funkcija.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.3. Nenoteiktā integrāļa pamatīpašības
Augstāk: 1. NENOTEIKTAIS INTEGRĀLIS
Iepriekšējais: 1.1. Primitīvā funkcija un nenoteiktais integrālis
2002-11-06