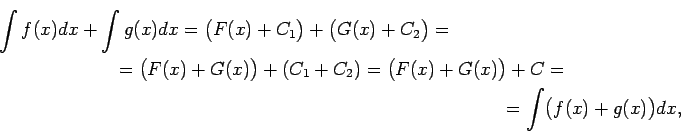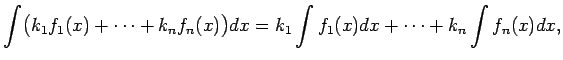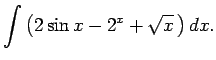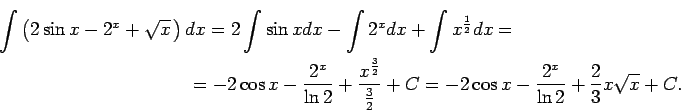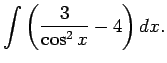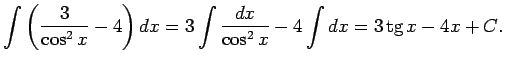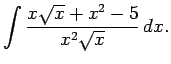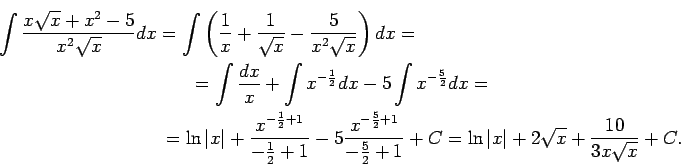Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.4. Integrēšanas pamatmetodes
Augstāk: 1. NENOTEIKTAIS INTEGRĀLIS
Iepriekšējais: 1.2. Pamatintegrāļu tabula
Izmantojot pamatintegrāļu tabulu, var integrēt tikai
visvienkāršākās funkcijas.
Piemēram,
Nenoteiktā integrāļa īpašības dod iespēju aprēķināt nenoteiktos
integrāļus ievērojami plašākai funkciju klasei.
- 1. īpašība.
- Nenoteiktā integrāļa atvasinājums ir vienāds ar
zemintegrāļa funkciju, t.i.,
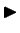 Šo īpašību pierāda, izmantojot nenoteiktā
integrāļa definīciju un diferencēšanas likumus.
Konkrēti:
Šo īpašību pierāda, izmantojot nenoteiktā
integrāļa definīciju un diferencēšanas likumus.
Konkrēti:
- 2ipa2. īpašība.
- Nenoteiktā integrāļa diferenciālis ir vienāds
ar
zemintegrāļa izteiksmi, t.i.,
- 3ipa3. īpašība.
- Nenoteiktais integrālis no funkcijas
 atvasinājuma
ir vienāds ar šo funkciju (ar precizitāti līdz konstantam saskaitāmajam
atvasinājuma
ir vienāds ar šo funkciju (ar precizitāti līdz konstantam saskaitāmajam 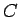 ), t.i.,
), t.i.,
- 4ipa4. īpašība.
- Nenoteiktais integrālis no funkcijas
 diferenciāļa ir vienāds ar šo funkciju (ar precizitāti līdz konstantam saskaitāmajam
diferenciāļa ir vienāds ar šo funkciju (ar precizitāti līdz konstantam saskaitāmajam
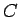 ), t.i.,
), t.i.,
-
1.1. piezīme.
- 2ipa2., 3ipa3. un
4ipa4. īpašību pierādīt patstāvīgi.
- 5ipa5. īpašība.
- Konstantu reizinātāju
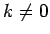 drīkst iznest
ārpus nenoteiktā integrāļa zīmes, t.i.,
drīkst iznest
ārpus nenoteiktā integrāļa zīmes, t.i.,
 Apzīmē funkcijas
Apzīmē funkcijas  primitīvo funkciju ar
primitīvo funkciju ar
 . Acīmredzami,
. Acīmredzami, 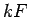 ir funkcijas
ir funkcijas 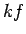 primitīvā funkcija.
Saskaņā ar nenoteiktā integrāļa definīciju
primitīvā funkcija.
Saskaņā ar nenoteiktā integrāļa definīciju
(Ja 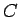 - patvaļīga konstante, tad
- patvaļīga konstante, tad
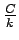 arī ir patvaļīga
konstante.)
arī ir patvaļīga
konstante.)
- 6ipa6. īpašība.
- Nenoteiktais integrālis no divu
funkciju
 un
un
 summas ir vienāds ar šo funkciju nenoteikto integrāļu summu, t.i.,
summas ir vienāds ar šo funkciju nenoteikto integrāļu summu, t.i.,
 Apzīmē funkciju
Apzīmē funkciju  un
un 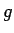 primitīvās funkcijas
atbilstoši ar
primitīvās funkcijas
atbilstoši ar  un
un 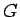 .
.
Acīmredzami, funkcijas 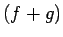 primitīvā funkcija ir funkcija
primitīvā funkcija ir funkcija
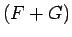 . Saskaņā ar nenoteiktā integrāļa definīciju
. Saskaņā ar nenoteiktā integrāļa definīciju
kur
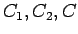 ir patvaļīgas konstantes, pie tam
ir patvaļīgas konstantes, pie tam 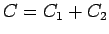 .
.
No 5ipa5. un 6ipa6. īpašības seko vēl
viena nenoteiktā integrāļa īpašība.
- 7. īpašība.
- Nenoteiktais integrālis no funkciju
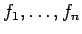 lineārās kombinācijas ir vienāds šo funkciju
nenoteikto integrāļu
lineāro kombināciju, t.i.,
kur vismaz viena no konstantēm
lineārās kombinācijas ir vienāds šo funkciju
nenoteikto integrāļu
lineāro kombināciju, t.i.,
kur vismaz viena no konstantēm
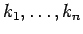 nav nulle.
nav nulle.
-
1.1. piemērs.
- Atrast
-
1.2. piemērs.
- Atrast
-
1.3. piemērs.
- Atrast



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.4. Integrēšanas pamatmetodes
Augstāk: 1. NENOTEIKTAIS INTEGRĀLIS
Iepriekšējais: 1.2. Pamatintegrāļu tabula
2002-11-06
![$\displaystyle \int\frac{dx}{\sqrt[3]{x^2}}=\int x^{-\frac{2}{3}}dx=
\frac{x^{-\frac{2}{3}+1}}{-\frac{2}{3}+1}+C=3\sqrt[3]{x}+C\/.$](img65.gif)
![$\displaystyle \int\frac{dx}{\sqrt[3]{x^2}}=\int x^{-\frac{2}{3}}dx=
\frac{x^{-\frac{2}{3}+1}}{-\frac{2}{3}+1}+C=3\sqrt[3]{x}+C\/.$](img65.gif)
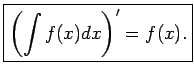
![]() Šo īpašību pierāda, izmantojot nenoteiktā
integrāļa definīciju un diferencēšanas likumus.
Konkrēti:
Šo īpašību pierāda, izmantojot nenoteiktā
integrāļa definīciju un diferencēšanas likumus.
Konkrēti:
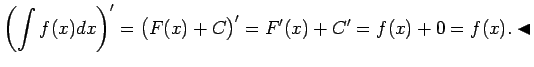
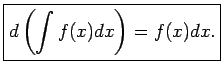
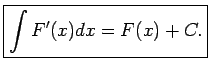
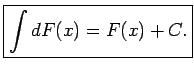
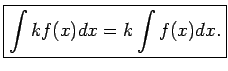
![]() Apzīmē funkcijas
Apzīmē funkcijas ![]() primitīvo funkciju ar
primitīvo funkciju ar
![]() . Acīmredzami,
. Acīmredzami, ![]() ir funkcijas
ir funkcijas ![]() primitīvā funkcija.
Saskaņā ar nenoteiktā integrāļa definīciju
primitīvā funkcija.
Saskaņā ar nenoteiktā integrāļa definīciju
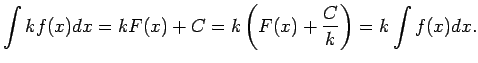
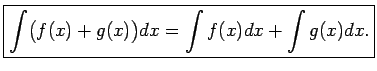
![]() Apzīmē funkciju
Apzīmē funkciju ![]() un
un ![]() primitīvās funkcijas
atbilstoši ar
primitīvās funkcijas
atbilstoši ar ![]() un
un ![]() .
.