


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.2. Pamatintegrāļu tabula
Augstāk: 1. NENOTEIKTAIS INTEGRĀLIS
Iepriekšējais: 1. NENOTEIKTAIS INTEGRĀLIS
Diferenciālrēķinu pamatuzdevums ir dotajai funkcijai atrast
atvasināto funkciju jeb atvasinājumu. Šis uzdevums ir atrisināms
viennozīmīgi. Bieži nepieciešams atrisināt arī apgrieztu uzdevumu -
pēc atvasinājuma atrast pašu funkciju. Izrādās, ka šis uzdevums nav
atrisināms viennozīmīgi, bet ar precizitāti līdz konstantam
saskaitāmajam.
Apskata divas funkcijas  un
un  , kas ir definētas intervālā
, kas ir definētas intervālā
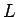 , pie tam funkcijai
, pie tam funkcijai  šajā intervālā eksistē atvasinājums.
šajā intervālā eksistē atvasinājums.
-
1.1. definīcija.
- Funkciju
 sauc par funkcijas
sauc par funkcijas  primitīvo
funkciju intervālā
primitīvo
funkciju intervālā 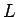 , ja visiem
, ja visiem 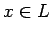 ir spēkā vienādība
ir spēkā vienādība
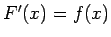 .
.
Piemēram, 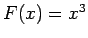 ir funkcijas
ir funkcijas 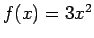 primitīvā funkcija.
Abas funkcijas definētas visu reālo skaitļu kopā
primitīvā funkcija.
Abas funkcijas definētas visu reālo skaitļu kopā
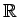 un
visiem
un
visiem
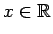 ir spēkā vienādība
ir spēkā vienādība
Acīmredzot, arī funkcija
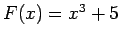 ir funkcijas
ir funkcijas 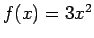 primitīvā funkcija. Vispār, dotās funkcijas primitīvā
funkcija ir funkcija
primitīvā funkcija. Vispār, dotās funkcijas primitīvā
funkcija ir funkcija
kur 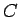 ir patvaļīga
konstante.
ir patvaļīga
konstante.
Dotās funkcijas primitīvo funkciju atrašana ir viens no
integrālrēķinu pamatuzdevumiem.
Funkcijas  divas primitīvās funkcijas viena no otras var
atšķirties tikai ar konstantu saskaitāmo (Pierādīt patstāvīgi).
divas primitīvās funkcijas viena no otras var
atšķirties tikai ar konstantu saskaitāmo (Pierādīt patstāvīgi).
-
1.2. definīcija.
- Funkcijas
 primitīvās funkcijas vispārīgo veidu
primitīvās funkcijas vispārīgo veidu
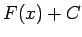 , kur
, kur  ir funkcijas
ir funkcijas  kāda primitīvā funkcija, bet
kāda primitīvā funkcija, bet
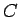 ir patvaļīga konstante, sauc par funkcijas
ir patvaļīga konstante, sauc par funkcijas  nenoteikto
integrāli un apzīmē ar simbolu
nenoteikto
integrāli un apzīmē ar simbolu
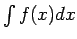 ,
t.i.,
,
t.i.,
Šajā formulā
 sauc par zemintegrāļa
funkciju,
sauc par zemintegrāļa
funkciju,
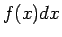 - par zemintegrāļa
izteiksmi,
- par zemintegrāļa
izteiksmi,
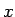 - par integrēšanas
mainīgo,
- par integrēšanas
mainīgo,
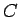 - par integrēšanas
konstanti.
- par integrēšanas
konstanti.
Simbols 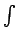 ir integrēšanas darbības simbols
(lasa:"integrālis ef no iks de iks").
ir integrēšanas darbības simbols
(lasa:"integrālis ef no iks de iks").
Piemēram,
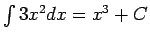 .
.
-
1.3. definīcija.
- Nenoteiktā integrāļa jeb visu primitīvo funkciju kopas
atrašanu dotajai funkcijai sauc par šīs funkcijas integrēšanu.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.2. Pamatintegrāļu tabula
Augstāk: 1. NENOTEIKTAIS INTEGRĀLIS
Iepriekšējais: 1. NENOTEIKTAIS INTEGRĀLIS
2002-11-06
![]() ir funkcijas
ir funkcijas ![]() primitīvā funkcija.
Abas funkcijas definētas visu reālo skaitļu kopā
primitīvā funkcija.
Abas funkcijas definētas visu reālo skaitļu kopā
![]() un
visiem
un
visiem
![]() ir spēkā vienādība
ir spēkā vienādība
![]() ir funkcijas
ir funkcijas ![]() primitīvā funkcija. Vispār, dotās funkcijas primitīvā
funkcija ir funkcija
primitīvā funkcija. Vispār, dotās funkcijas primitīvā
funkcija ir funkcija
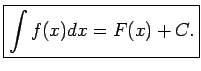
![]() sauc par zemintegrāļa
funkciju,
sauc par zemintegrāļa
funkciju,
![]() - par zemintegrāļa
izteiksmi,
- par zemintegrāļa
izteiksmi,
![]() - par integrēšanas
mainīgo,
- par integrēšanas
mainīgo,
![]() - par integrēšanas
konstanti.
- par integrēšanas
konstanti.