


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2. FUNKCIJA
Augstāk: 1.5. Apkārtnes kopā
Iepriekšējais: 1.6. Jautājumi
- Nosaukt divu tādu kopu piemērus, lai viena kopa atrastos
pa kreisi no otras kopas.
- Nosaukt divu tādu kopu piemērus, lai tās atdalītu vismaz
viens skaitlis; lai tās atdalītu viens skaitlis.
- Konstruēt funkciju grafikus:
-
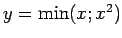 ;
;
-
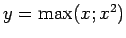 ;
;
-
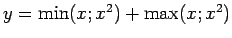 ;
;
-
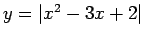 ;
;
-
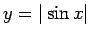 ;
;
-
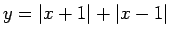 ;
;
-
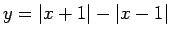 ;
;
- Atrisināt nevienādības:
-
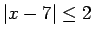 ;
;
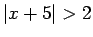 ;
;
-
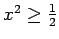 ;
;
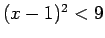 .
.
- Atrisināt vienādojumus:
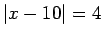 ;
;
-
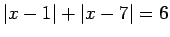 .
.
- Nosaukt moduļa īpašības.
- Pierādīt, ka triju reālu skaitļu summas modulis
nepārsniedz šo skaitļu moduļu summu.
- Pierādīt, ka triju reālu skaitļu reizinājuma modulis ir
vienāds ar šo skaitļu moduļu reizinājumu.
- Pamatot, ka
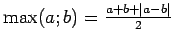 , bet
, bet
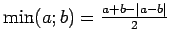 .
.
- Nosaukt ierobežotas no augšas, ierobežotas no apakšas un
ierobežotas kopas piemērus.
- Pierādīt, ka kopa
 ir ierobežota tad un tikai tad,
kad ir ierobežota no augšas kopa, kas sastādīta no šīs kopas
elementu moduļiem.
ir ierobežota tad un tikai tad,
kad ir ierobežota no augšas kopa, kas sastādīta no šīs kopas
elementu moduļiem.
- Konstruēt kopu, kurai apakšējais slieksnis tai pieder,
bet augšējais slieksnis tai nepieder.
- Dota šādu intervālu kopa
![$ [a_1;b_1]\supset[a_2;b_2]\supset\cdots\supset[a_n;b_n]\supset\cdots$](img160.gif) .
Pierādīt, ka visiem šiem intervāliem eksistē vismaz viens
kopīgs punkts
.
Pierādīt, ka visiem šiem intervāliem eksistē vismaz viens
kopīgs punkts 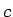 .
.
- Pierādīt apkārtņu īpašības (ka divu punkta
 apkārtņu šķēlums
ir šī punkta apkārtne; ka jebkuri divi dažādi
apkārtņu šķēlums
ir šī punkta apkārtne; ka jebkuri divi dažādi
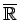 punkti ir atdalāmi ar
apkārtnēm).
punkti ir atdalāmi ar
apkārtnēm).



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2. FUNKCIJA
Augstāk: 1.5. Apkārtnes kopā
Iepriekšējais: 1.6. Jautājumi
2003-02-24
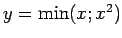 ;
;
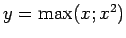 ;
;
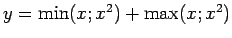 ;
;
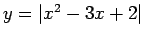 ;
;
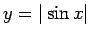 ;
;
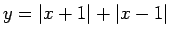 ;
;
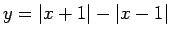 ;
;
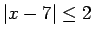 ;
;
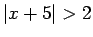 ;
;
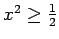 ;
;
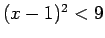 .
.
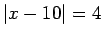 ;
;
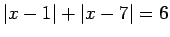 .
.
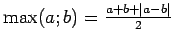 , bet
, bet
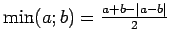 .
.
 ir ierobežota tad un tikai tad,
kad ir ierobežota no augšas kopa, kas sastādīta no šīs kopas
elementu moduļiem.
ir ierobežota tad un tikai tad,
kad ir ierobežota no augšas kopa, kas sastādīta no šīs kopas
elementu moduļiem.
![$ [a_1;b_1]\supset[a_2;b_2]\supset\cdots\supset[a_n;b_n]\supset\cdots$](img160.gif) .
Pierādīt, ka visiem šiem intervāliem eksistē vismaz viens
kopīgs punkts
.
Pierādīt, ka visiem šiem intervāliem eksistē vismaz viens
kopīgs punkts 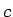 .
.
 apkārtņu šķēlums
ir šī punkta apkārtne; ka jebkuri divi dažādi
apkārtņu šķēlums
ir šī punkta apkārtne; ka jebkuri divi dažādi
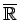 punkti ir atdalāmi ar
apkārtnēm).
punkti ir atdalāmi ar
apkārtnēm).