


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.3. Saliktas funkcijas nepārtrauktība
Augstāk: 2. VAIRĀKU ARGUMENTU FUNKCIJAS ROBEŽA UN
Iepriekšējais: 2.1. Vairāku argumentu funkcijas robeža
Uzskata, ka vairāku argumentu funkcija 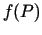 ir definēta punkta
ir definēta punkta
 kaut kādā apkārtnē, ieskaitot arī pašu punktu
kaut kādā apkārtnē, ieskaitot arī pašu punktu  .
.
-
2.4. definīcija.
- Funkciju
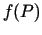 sauc par nepārtrauktu
punktā
sauc par nepārtrauktu
punktā  , ja
, ja
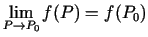 .
.
Izmantojot funkcijas robežas definīcijas (2.1. un
2.2. definīcija), var iegūt vēl divas punktā
nepārtrauktas funkcijas definīcijas.
-
2.5. definīcija.
- Funkciju
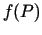 sauc par nepārtrauktu
punktā
sauc par nepārtrauktu
punktā  , ja jebkuram
, ja jebkuram
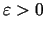 eksistē tāds
eksistē tāds 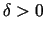 , ka visiem
, ka visiem 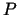 , kuriem
, kuriem
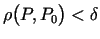 , izpildās nevienādība
, izpildās nevienādība
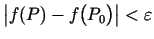 .
.
-
2.6. definīcija.
- Funkciju
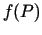 sauc par nepārtrauktu
punktā
sauc par nepārtrauktu
punktā  , ja jebkuram
, ja jebkuram
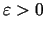 eksistē tāds
eksistē tāds 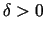 , ka visiem
, ka visiem 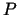 , kas pieder punkta
, kas pieder punkta 
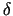 - apkārtnei, ir spēkā nevienādība
- apkārtnei, ir spēkā nevienādība
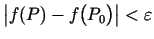 .
.
Tāpat kā viena argumenta funkcijām, arī vairāku argumentu
nepārtrauktām funkcijām ir spēkā šādas teorēmas (pierādījumi
arī ir analoģiski).
-
2.6. teorēma.
- Ja funkcija ir nepārtraukta punktā,
tad tā ir ierobežota šī punkta kaut kādā apkārtnē.
-
2.7. teorēma.
- Ja funkcija
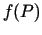 ir nepārtraukta
punktā
ir nepārtraukta
punktā  un
un
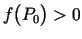
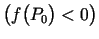 , tad eksistē šī punkta tāda
apkārtne, kurā
, tad eksistē šī punkta tāda
apkārtne, kurā 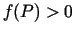
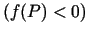 .
.
-
2.8. teorēma.
- Ja funkcijas
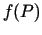 ,
, 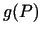 ir
nepārtrauktas punktā
ir
nepārtrauktas punktā  , tad šo funkciju summa, starpība,
reizinājums un dalījums ir nepārtrauktas šajā punktā funkcijas.
, tad šo funkciju summa, starpība,
reizinājums un dalījums ir nepārtrauktas šajā punktā funkcijas.
Lai izveidotu vēl vienu punktā nepārtrauktas funkcijas definīciju,
izmanto funkcijas pieaugumus.
Apskata, piemēram, divu argumentu funkciju  , kas
definēta punkta
, kas
definēta punkta
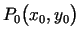 kaut kādā apkārtnē.
Argumentiem
kaut kādā apkārtnē.
Argumentiem 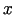 un
un 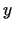 izvēlas patvaļīgus pieaugumus
izvēlas patvaļīgus pieaugumus 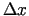 un
un
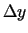 , bet tādus, lai punkts
, bet tādus, lai punkts
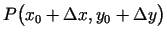 arī piederētu šai apkārtnei (2.3. zīm.).
arī piederētu šai apkārtnei (2.3. zīm.).
Starpību
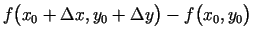 sauc par funkcijas
sauc par funkcijas  pilno pieaugumu punktā
pilno pieaugumu punktā
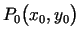 , kas atbilst
argumentu pieaugumiem
, kas atbilst
argumentu pieaugumiem 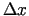 un
un 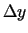 , un apzīmē ar
, un apzīmē ar
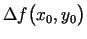 jeb
jeb
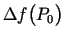 (īsāk
(īsāk
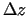 ). Starpību
). Starpību
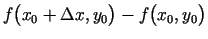 sauc par funkcijas
sauc par funkcijas  parciālo pieaugumu
punktā
parciālo pieaugumu
punktā
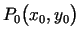 pēc
pēc
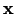 , bet
, bet
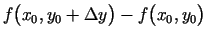 - funkcijas
- funkcijas
 parciālo pieaugumu punktā
parciālo pieaugumu punktā
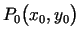 pēc
pēc
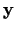 . Šos parciālos
pieaugumus apzīmē atbilstoši ar
. Šos parciālos
pieaugumus apzīmē atbilstoši ar
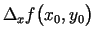 un
un
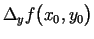 (īsāk
(īsāk
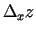 ,
,
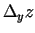 ).
).
Tādējādi (skat. 2.3. zīm.)
-
2.4. piezīme.
- Analoģiski definē triju argumentu funkcijas
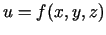 pilno pieaugumu
pilno pieaugumu 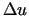 un parciālos pieaugumus
un parciālos pieaugumus
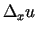 ,
,
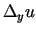 un
un
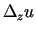 .
.
-
2.7. definīcija.
- Divu argumentu funkciju
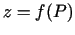 sauc par
nepārtrauktu punktā
sauc par
nepārtrauktu punktā  , ja funkcijas pilnais pieaugums
, ja funkcijas pilnais pieaugums
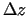 punktā
punktā  ir bezgalīgi maza funkcija, kad
ir bezgalīgi maza funkcija, kad
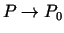 (
(
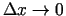 un
un
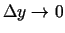 ), t.i.,
), t.i.,
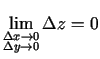 .
.
-
2.5. piezīme.
- Ja
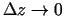 , tad acīmredzami,
, tad acīmredzami,
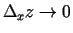 . Apgrieztais apgalvojums nav spēkā (skat. 12. vingr.).
. Apgrieztais apgalvojums nav spēkā (skat. 12. vingr.).



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.3. Saliktas funkcijas nepārtrauktība
Augstāk: 2. VAIRĀKU ARGUMENTU FUNKCIJAS ROBEŽA UN
Iepriekšējais: 2.1. Vairāku argumentu funkcijas robeža
2002-06-21
![]() ir definēta punkta
ir definēta punkta
![]() kaut kādā apkārtnē, ieskaitot arī pašu punktu
kaut kādā apkārtnē, ieskaitot arī pašu punktu ![]() .
.
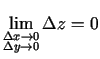 .
.