Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3. VAIRĀKU ARGUMENTU DIFERENCĒJAMAS FUNKCIJAS
Augstāk: 2. VAIRĀKU ARGUMENTU FUNKCIJAS ROBEŽA UN
Iepriekšējais: 2.5. Jautājumi
- Pierādīt, ka
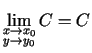 (
(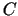 - konstante) un
- konstante) un
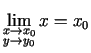 .
.
- Formulēt apkārtņu svarīgākās īpašības.
- Pierādīt funkcijas
 robežas vienīgumu.
robežas vienīgumu.
- Pierādīt, ka funkcija, kurai eksistē robeža, ir ierobežota
funkcija.
- Pierādīt teorēmu par robežpāreju nevienādībās.
- Pierādīt teorēmu par mainīgā starplieluma robežu.
- Pierādīt teorēmu par divu funkciju summas robežu.
- Izskaitļot robežas:
a)
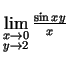 ;
;
b)
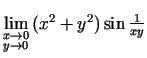 ;
;
c)
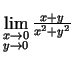 ;
;
d)
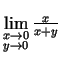 ;
;
e)
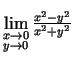 .
.
- Definēt triju argumentu funkcijas pilno un parciālos
pieaugumus.
- Atrast funkciju pilno un parciālos pieaugumus punktā
 .
.
a)
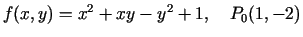 ;
;
b)
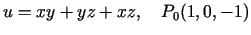 .
.
- Kā izmainīsies taisnstūra diagonāle, ja vienu taisnstūra malu
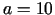 cm pagarināt par
cm pagarināt par 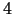 mm, bet otru -
mm, bet otru - 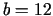 cm saīsināt par
cm saīsināt par
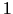 mm?
mm?
- Parādīt, ka funkcija
ir nepārtraukta punktā
 pēc katra no mainīgiem
pēc katra no mainīgiem 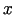 un
un 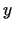 ,
apskatot tos atsevišķi, bet nav nepārtraukta šajā punktā kā divu
mainīgo funkcija.
,
apskatot tos atsevišķi, bet nav nepārtraukta šajā punktā kā divu
mainīgo funkcija.
- Atrast funkcijas
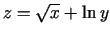 definīcijas apgabalu.
Norādīt tā iekšējos, ārējos un robežas punktus.
definīcijas apgabalu.
Norādīt tā iekšējos, ārējos un robežas punktus.
- Atrast funkciju definīcijas apgabalus un noskaidrot, vai
iegūtās kopas ir slēgtas, vaļējas, sakarīgas, ierobežotas.
a)
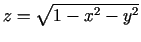 ;
;
b)
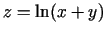 ;
;
c)
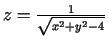 ;
;
d)
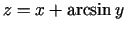 ;
;
e)
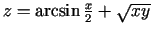 ;
;
f)
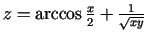 .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3. VAIRĀKU ARGUMENTU DIFERENCĒJAMAS FUNKCIJAS
Augstāk: 2. VAIRĀKU ARGUMENTU FUNKCIJAS ROBEŽA UN
Iepriekšējais: 2.5. Jautājumi
2002-06-21
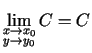 (
(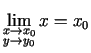 .
.
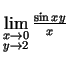 ;
;
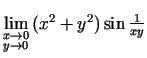 ;
;
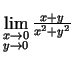 ;
;
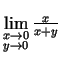 ;
;
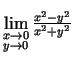 .
.
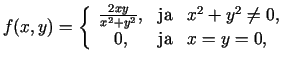
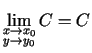 (
(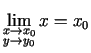 .
.
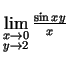 ;
;
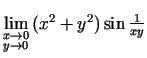 ;
;
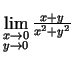 ;
;
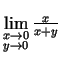 ;
;
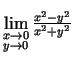 .
.