


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.5. Jautājumi
Augstāk: 2. VAIRĀKU ARGUMENTU FUNKCIJAS ROBEŽA UN
Iepriekšējais: 2.3. Saliktas funkcijas nepārtrauktība
-
2.8. definīcija.
- Punktu
 sauc par kopas
sauc par kopas  iekšējo
punktu, ja eksistē šī punkta tāda apkārtne, kas iekļaujas kopā
iekšējo
punktu, ja eksistē šī punkta tāda apkārtne, kas iekļaujas kopā
 .
.
-
2.9. definīcija.
- Punktu
 sauc par kopas
sauc par kopas  ārējo punktu, ja eksistē šī punkta tāda apkārtne, kas nesatur nevienu
kopas
ārējo punktu, ja eksistē šī punkta tāda apkārtne, kas nesatur nevienu
kopas  punktu.
punktu.
-
2.10. definīcija.
- Punktu
 sauc par kopas
sauc par kopas  robežas punktu, ja šī punkta jebkura apkārtne satur gan kopai
robežas punktu, ja šī punkta jebkura apkārtne satur gan kopai  piederošos, gan kopai
piederošos, gan kopai  nepiederošos punktus.
nepiederošos punktus.
-
2.8. piezīme.
-

- 2.4. zīmējumā punkts
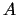 ir kopas
ir kopas  iekšējais,
iekšējais, 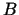 - kopas
- kopas
 ārējais, bet
ārējais, bet 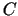 - kopas
- kopas  robežas punkts.
robežas punkts.
- Acīmredzami katrs kopas iekšējais punkts pieder šai kopai,
bet kopas robežas punkts var gan piederēt, gan nepiederēt šai kopai
(skat. 2.4., 2.5. zīm.).
Piemēram, kopu  veido koordinātu plaknes tie punkti, kuri
apmierina nevienādību
veido koordinātu plaknes tie punkti, kuri
apmierina nevienādību
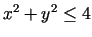 . Šīs kopas robežas punkti ir
riņķa līnijas
. Šīs kopas robežas punkti ir
riņķa līnijas 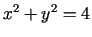 punkti, kas pieder
punkti, kas pieder  .
.
-
2.11. definīcija.
- Kopu
 sauc par slēgtu
kopu, ja tā satur visus savus robežas punktus.
sauc par slēgtu
kopu, ja tā satur visus savus robežas punktus.
-
2.9. piezīme.
- Kopa
 , kas apskatīta iepriekšējā piemērā, ir slēgta
kopa.
, kas apskatīta iepriekšējā piemērā, ir slēgta
kopa.
-
2.12. definīcija.
- Kopu
 sauc par vaļēju
kopu, ja tā nesatur nevienu savu robežas punktu.
sauc par vaļēju
kopu, ja tā nesatur nevienu savu robežas punktu.
-
2.10. piezīme.
- Vaļēja kopa sastāv tikai no saviem iekšējiem punktiem.
Piemēram, kopa  , kuru veido koordinātu plaknes tie punkti, kuri
apmierina nevienādību
, kuru veido koordinātu plaknes tie punkti, kuri
apmierina nevienādību 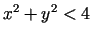 , ir vaļēja kopa.
, ir vaļēja kopa.
-
2.11. piezīme.
- Eksistē tādas kopas, kuras nav ne vaļējas, ne slēgtas
kopas.
Piemēram, kopa  , kuru veido koordinātu plaknes tie punkti, kas
apmierina nevienādību
, kuru veido koordinātu plaknes tie punkti, kas
apmierina nevienādību
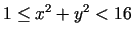 (2.5. zīm.) nav ne
vaļēja, ne slēgta kopa.
(2.5. zīm.) nav ne
vaļēja, ne slēgta kopa.
-
2.13. definīcija.
- Kopu
 sauc par sakarīgu
kopu, ja šīs kopas jebkurus divus punktus var savienot ar lauztu līniju
(šai lauztai līnijai posmu skaits ir galīgs), kas iekļaujas kopā
sauc par sakarīgu
kopu, ja šīs kopas jebkurus divus punktus var savienot ar lauztu līniju
(šai lauztai līnijai posmu skaits ir galīgs), kas iekļaujas kopā  .
.
-
2.12. piezīme.
-
 2.6. un 2.7. zīmējumā ir attēlotas sakarīgas kopas
koordinātu plaknē.
2.6. un 2.7. zīmējumā ir attēlotas sakarīgas kopas
koordinātu plaknē.
-
2.14. definīcija.
- Kopu
 sauc par ierobežotu
kopu, ja eksistē tāds skaitlis
sauc par ierobežotu
kopu, ja eksistē tāds skaitlis 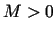 , ka visiem
, ka visiem 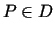 izpildās
nevienādība
izpildās
nevienādība
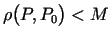 , kur
, kur  - kopas
- kopas  fiksēts punkts.
fiksēts punkts.
-
2.13. piezīme.
- Ja ierobežota kopa
 atrodas plaknē (telpā), tad,
acīmredzami, eksistē tāds vaļējs riņķis (vaļēja lode) ar centru
punktā
atrodas plaknē (telpā), tad,
acīmredzami, eksistē tāds vaļējs riņķis (vaļēja lode) ar centru
punktā  un rādiusu
un rādiusu 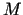 , kas satur kopu
, kas satur kopu  .
.
Definējot punktā  nepārtrauktu funkciju, uzskatīja, ka
nepārtrauktu funkciju, uzskatīja, ka  ir funkcijas definīcijas apgabala iekšējais punkts.
ir funkcijas definīcijas apgabala iekšējais punkts.
Atliek definēt punktā  nepārtrauktu funkciju, ja
nepārtrauktu funkciju, ja  ir
funkcijas definīcijas apgabala
ir
funkcijas definīcijas apgabala  robežas punkts, pie tam
robežas punkts, pie tam
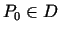 .
.
-
2.15. definīcija.
- Funkciju
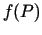 sauc par nepārtrauktu
tās definīcijas apgabala
sauc par nepārtrauktu
tās definīcijas apgabala  robežas punktā
robežas punktā 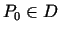 , ja jebkuram
, ja jebkuram
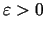 eksistē tāds
eksistē tāds 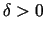 ,
ka visiem
,
ka visiem 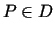 , kuriem izpildās nevienādība
, kuriem izpildās nevienādība
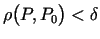 , ir spēkā nevienādība
, ir spēkā nevienādība
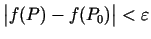 .
.
-
2.16. definīcija.
- Funkciju
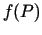 , kas nepārtraukta
kopas katrā punktā, sauc par kopā
, kas nepārtraukta
kopas katrā punktā, sauc par kopā  nepārtrauktu
funkciju.
nepārtrauktu
funkciju.
Slēgtā un ierobežotā kopā nepārtrauktu vairāku argumentu funkciju
īpašības ir analogas slēgtā intervālā nepārtrauktu viena argumenta
funkciju īpašībām.
- 1. īpašība.
- (Veierštrāsa 1. teorēma).
Ja funkcija 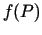 ir nepārtraukta slēgtā un
ierobežotā kopā
ir nepārtraukta slēgtā un
ierobežotā kopā  , tad tā ir ierobežota šajā kopā.
, tad tā ir ierobežota šajā kopā.
- 2. īpašība.
- (Veierštrāsa 2. teorēma).
Ja funkcija 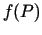 ir nepārtraukta slēgtā un
ierobežotā kopā
ir nepārtraukta slēgtā un
ierobežotā kopā  , tad tā sasniedz šajā kopā savu vismazāko un vislielāko vērtību.
, tad tā sasniedz šajā kopā savu vismazāko un vislielāko vērtību.
Ja  - sakarīga kopa un
- sakarīga kopa un 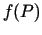 - nepārtraukta funkcija šajā
kopā, tad ir spēkā Bolcano teorēma par nepārtrauktas funkcijas
starpvērtībām.
- nepārtraukta funkcija šajā
kopā, tad ir spēkā Bolcano teorēma par nepārtrauktas funkcijas
starpvērtībām.
-
2.10. teorēma.
- (Bolcano teorēma).
Ja sakarīgā kopā  nepārtraukta funkcija
nepārtraukta funkcija 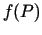 šīs kopas divos
punktos
šīs kopas divos
punktos 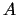 un
un 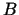 pieņem dažādas vērtības,
pieņem dažādas vērtības,
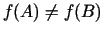 , tad kāds arī
nebūtu skaitlis
, tad kāds arī
nebūtu skaitlis 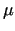 starp
starp 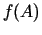 un
un 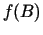 eksistē
eksistē 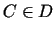 , ka
, ka
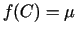 .
.
- Sekas.
- (Par nepārtrauktas funkcijas nullēm).
Ja sakarīgā kopā  nepārtraukta funkcija
nepārtraukta funkcija 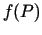 šīs kopas divos
punktos
šīs kopas divos
punktos 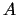 un
un 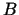 pieņem vērtības
pieņem vērtības 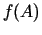 un
un 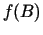 , kurām ir
pretējas zīmes, tad eksistē tāds punkts
, kurām ir
pretējas zīmes, tad eksistē tāds punkts 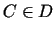 , ka
, ka 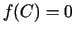 .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.5. Jautājumi
Augstāk: 2. VAIRĀKU ARGUMENTU FUNKCIJAS ROBEŽA UN
Iepriekšējais: 2.3. Saliktas funkcijas nepārtrauktība
2002-06-21
![]() veido koordinātu plaknes tie punkti, kuri
apmierina nevienādību
veido koordinātu plaknes tie punkti, kuri
apmierina nevienādību
![]() . Šīs kopas robežas punkti ir
riņķa līnijas
. Šīs kopas robežas punkti ir
riņķa līnijas ![]() punkti, kas pieder
punkti, kas pieder ![]() .
.
![]() , kuru veido koordinātu plaknes tie punkti, kuri
apmierina nevienādību
, kuru veido koordinātu plaknes tie punkti, kuri
apmierina nevienādību ![]() , ir vaļēja kopa.
, ir vaļēja kopa.
![]() , kuru veido koordinātu plaknes tie punkti, kas
apmierina nevienādību
, kuru veido koordinātu plaknes tie punkti, kas
apmierina nevienādību
![]() (2.5. zīm.) nav ne
vaļēja, ne slēgta kopa.
(2.5. zīm.) nav ne
vaļēja, ne slēgta kopa.
![]() nepārtrauktu funkciju, uzskatīja, ka
nepārtrauktu funkciju, uzskatīja, ka ![]() ir funkcijas definīcijas apgabala iekšējais punkts.
ir funkcijas definīcijas apgabala iekšējais punkts.
![]() ir nepārtraukta slēgtā un
ierobežotā kopā
ir nepārtraukta slēgtā un
ierobežotā kopā ![]() , tad tā ir ierobežota šajā kopā.
, tad tā ir ierobežota šajā kopā.
![]() ir nepārtraukta slēgtā un
ierobežotā kopā
ir nepārtraukta slēgtā un
ierobežotā kopā ![]() , tad tā sasniedz šajā kopā savu vismazāko un vislielāko vērtību.
, tad tā sasniedz šajā kopā savu vismazāko un vislielāko vērtību.
![]() - sakarīga kopa un
- sakarīga kopa un ![]() - nepārtraukta funkcija šajā
kopā, tad ir spēkā Bolcano teorēma par nepārtrauktas funkcijas
starpvērtībām.
- nepārtraukta funkcija šajā
kopā, tad ir spēkā Bolcano teorēma par nepārtrauktas funkcijas
starpvērtībām.
![]() nepārtraukta funkcija
nepārtraukta funkcija ![]() šīs kopas divos
punktos
šīs kopas divos
punktos ![]() un
un ![]() pieņem dažādas vērtības,
pieņem dažādas vērtības,
![]() , tad kāds arī
nebūtu skaitlis
, tad kāds arī
nebūtu skaitlis ![]() starp
starp ![]() un
un ![]() eksistē
eksistē ![]() , ka
, ka
![]() .
.
![]() nepārtraukta funkcija
nepārtraukta funkcija ![]() šīs kopas divos
punktos
šīs kopas divos
punktos ![]() un
un ![]() pieņem vērtības
pieņem vērtības ![]() un
un ![]() , kurām ir
pretējas zīmes, tad eksistē tāds punkts
, kurām ir
pretējas zīmes, tad eksistē tāds punkts ![]() , ka
, ka ![]() .
.