Apskata kopā
Apskata kopā ![]() definētu funkciju
definētu funkciju
![]() , kur
, kur
![]() un
un
![]() ir kopā
ir kopā ![]() definētas funkcijas. Ja
visiem
definētas funkcijas. Ja
visiem
![]() vērtības
vērtības ![]() un
un ![]() ir tādas, ka
ir tādas, ka
![]() , tad saka, ka kopā
, tad saka, ka kopā ![]() ir definēta salikta
funkcija
ir definēta salikta
funkcija ![]() , kur
, kur ![]() ,
, ![]() . Šo salikto
funkciju var uzrakstīt
. Šo salikto
funkciju var uzrakstīt
![]() .
.
Piemēram,
Piemēram, ![]() , kur
, kur
![]() ,
, ![]() ir salikta
funkcija. Starpargumenti ir
ir salikta
funkcija. Starpargumenti ir ![]() un
un ![]() , bet neatkarīgie
mainīgie -
, bet neatkarīgie
mainīgie - ![]() .
.
Ja kopā ![]() ir definēta salikta funkcija
ir definēta salikta funkcija ![]() ,
kur
,
kur ![]() ,
,
![]() , funkcijas
, funkcijas ![]() ,
, ![]() - nepārtrauktas punktā
- nepārtrauktas punktā
![]() un
un ![]() - nepārtraukta atbilstošajā punktā
- nepārtraukta atbilstošajā punktā
![]() , kur
, kur
![]() ,
,
![]() ,
tad salikta funkcija
,
tad salikta funkcija
![]() Apzīmē ar
Apzīmē ar
![]() attālumu
starp punktiem
attālumu
starp punktiem ![]() un
un
![]() . Ir zināms, ka
. Ir zināms, ka
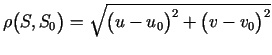 .
Tā kā funkcija
.
Tā kā funkcija ![]() ir nepārtraukta punktā
ir nepārtraukta punktā
![]() , tad saskaņā ar definīciju jebkuram
, tad saskaņā ar definīciju jebkuram
![]() eksistē tāds
eksistē tāds
![]() , ka no nevienādības
, ka no nevienādības
![]() seko nevienādība
seko nevienādība
![]() . Tā kā funkcijas
. Tā kā funkcijas ![]() un
un ![]() ir nepārtrauktas punktā
ir nepārtrauktas punktā
![]() , tad
dotajam
, tad
dotajam ![]() eksistē tādi
eksistē tādi ![]() un
un ![]() pozitīvi,
ka no nevienādībām
pozitīvi,
ka no nevienādībām
![]() un
un
![]() seko atbilstošas nevienādības
seko atbilstošas nevienādības
Apzīmē ar
Izmantojot šīs nevienādības, var iegūt, ka attālums
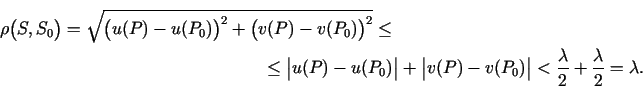
Tādējādi no nevienādības
![]() seko nevienādība
seko nevienādība
![]() , bet no tās seko nevienādība
, bet no tās seko nevienādība
![]() jeb
jeb
Šī nevienādība norāda, ka salikta funkcija
![]() ir nepārtraukta punktā
ir nepārtraukta punktā
![]() .
.
![]()