Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4.3. Jautājumi
Augstāk: 4. VAIRĀKU ARGUMENTU FUNKCIJU PĒTĪŠANA UZ
Iepriekšējais: 4.1. Vairāku argumentu funkcijas maksimums un
Iepriekš tika atzīmēts, ka slēgtā un ierobežotā kopā  nepārtraukta
funkcija ir ierobežota un sasniedz kopā
nepārtraukta
funkcija ir ierobežota un sasniedz kopā  vismazāko un vislielāko
vērtību.
vismazāko un vislielāko
vērtību.
Skaidrs, ka šīs vērtības funkcija var sasniegt  iekšējos punktos
(acīmredzami šie punkti ir funkcijas ekstrēma punkti) vai arī
iekšējos punktos
(acīmredzami šie punkti ir funkcijas ekstrēma punkti) vai arī
 robežas punktos.
robežas punktos.
Tāpēc, lai atrastu slēgtā un ierobežotā kopā  nepārtrauktas
funkcijas vislielāko un vismazāko vērtību, atrod kopas
nepārtrauktas
funkcijas vislielāko un vismazāko vērtību, atrod kopas  tos
iekšējos punktus, kuros izpildās ekstrēma nepieciešamais nosacījums
un izskaitļo funkcijas vērtības šajos punktos. Atrod arī funkcijas
vislielāko un vismazāko vērtību uz
tos
iekšējos punktus, kuros izpildās ekstrēma nepieciešamais nosacījums
un izskaitļo funkcijas vērtības šajos punktos. Atrod arī funkcijas
vislielāko un vismazāko vērtību uz  robežas (kopas
robežas (kopas  punktos
iegūst viena argumenta funkciju).
punktos
iegūst viena argumenta funkciju).
Visbeidzot no visām iegūtajām funkcijas vērtībām izvēlas mazāko
(apzīmē
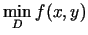 ) un lielāko vērtību (apzīmē
) un lielāko vērtību (apzīmē
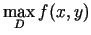 ).
).
-
4.5. piezīme.
- Ja kopa
 nav slēgta vai nav ierobežota, vai funkcija
nav nepārtraukta kopā
nav slēgta vai nav ierobežota, vai funkcija
nav nepārtraukta kopā  , tad funkcijai vislielākā vai vismazākā
vērtība var neeksistēt.
, tad funkcijai vislielākā vai vismazākā
vērtība var neeksistēt.
-
4.6. piemērs.
- Atrast funkcijas
vismazāko
un vislielāko vērtību kopā, kuru ierobežo taisnes
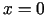 ,
, 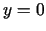 ,
,
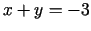 .
.
Vispirms kopu  attēlo grafiski (4.3. zīm.). Atrod
attēlo grafiski (4.3. zīm.). Atrod
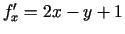 ,
,
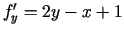 . Atrisina sistēmu
. Atrisina sistēmu
Funkcijas stacionārais punkts
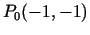 ir kopas
ir kopas  iekšējais punkts. Izskaitļo
iekšējais punkts. Izskaitļo
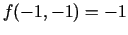 .
.
Pēta funkciju uz  robežas. (
robežas. ( robeža sastāv no
robeža sastāv no 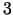 nogriežņiem).
nogriežņiem).
- Uz nogriežņa
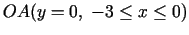
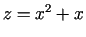 ,
,
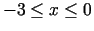 . Atrod
. Atrod 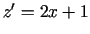 . Punkts
. Punkts
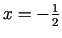 ir intervāla
ir intervāla ![$ [-3,0]$](img881.gif) iekšējais punkts, tāpēc izskaitļo
iekšējais punkts, tāpēc izskaitļo
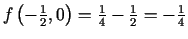 .
.
- Uz nogriežņa
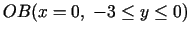
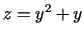 ,
,
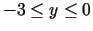 . Atrod
. Atrod 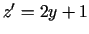 . Punkts
. Punkts
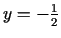 ir intervāla
ir intervāla ![$ [-3,0]$](img881.gif) iekšējais punkts, tāpēc izskaitļo
iekšējais punkts, tāpēc izskaitļo
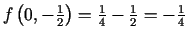 .
.
- Uz nogriežņa
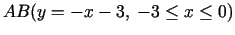
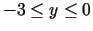 .
Atrod
.
Atrod 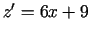 . Punkts
. Punkts
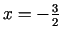 ir intervāla
ir intervāla ![$ [-3,0]$](img881.gif) iekšējais punkts, tāpēc izskaitļo
iekšējais punkts, tāpēc izskaitļo
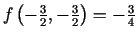 .
.
Visbeidzot izskaitļo funkcijas vērtības trijstūra 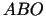 (kopas
(kopas  )
virsotnēs.
)
virsotnēs.
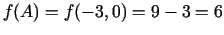 ;
;
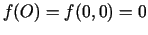 ;
;
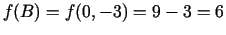 .
.
Tādējādi
un



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4.3. Jautājumi
Augstāk: 4. VAIRĀKU ARGUMENTU FUNKCIJU PĒTĪŠANA UZ
Iepriekšējais: 4.1. Vairāku argumentu funkcijas maksimums un
2002-06-21
![]() nepārtraukta
funkcija ir ierobežota un sasniedz kopā
nepārtraukta
funkcija ir ierobežota un sasniedz kopā ![]() vismazāko un vislielāko
vērtību.
vismazāko un vislielāko
vērtību.
![]() attēlo grafiski (4.3. zīm.). Atrod
attēlo grafiski (4.3. zīm.). Atrod
![]() ,
,
![]() . Atrisina sistēmu
. Atrisina sistēmu