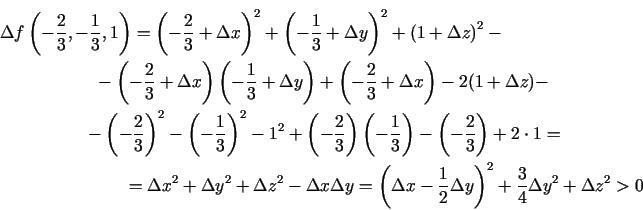Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4.2. Divu argumentu funkcijas vismazākās un
Augstāk: 4. VAIRĀKU ARGUMENTU FUNKCIJU PĒTĪŠANA UZ
Iepriekšējais: 4. VAIRĀKU ARGUMENTU FUNKCIJU PĒTĪŠANA UZ
Apskata punkta
 apkārtnē definētu funkciju
apkārtnē definētu funkciju  ,
kas nepārtraukta šajā punktā.
,
kas nepārtraukta šajā punktā.
-
4.1. definīcija.
- Ja visiem punktiem
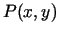 , kas pieder punkta
, kas pieder punkta
 apkārtnei un kas ir atšķirīgi no šī punkta, ir
spēkā
nevienādība
apkārtnei un kas ir atšķirīgi no šī punkta, ir
spēkā
nevienādība
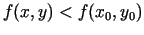 , tad
, tad
 sauc par šīs funkcijas maksimuma
punktu, bet funkcijas vērtību šajā punktā sauc par funkcijas
maksimumu un apzīmē
sauc par šīs funkcijas maksimuma
punktu, bet funkcijas vērtību šajā punktā sauc par funkcijas
maksimumu un apzīmē
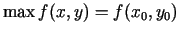 . Analoģiski definē
funkcijas minimuma punktu un tās minimumu.
. Analoģiski definē
funkcijas minimuma punktu un tās minimumu.
-
4.2. definīcija.
- Funkcijas maksimuma vai minimuma punktu sauc par funkcijas ekstrēma
punktu, bet funkcijas maksimumu vai minimumu sauc par funkcijas
ekstrēmu.
Piemēram, funkcijai
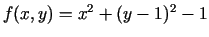 punkts
punkts 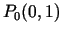 ir tās
minimuma punkts un
ir tās
minimuma punkts un
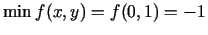 .
.
-
4.1. teorēma.
- (Funkcijas ekstrēma nepieciešamais
nosacījums).
Ja
 ir funkcijas
ir funkcijas  ekstrēma punkts, tad
šajā
punktā funkcijas parciālie atvasinājumi
ekstrēma punkts, tad
šajā
punktā funkcijas parciālie atvasinājumi
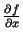 un
un
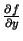 ir nulles (protams, ja tie eksistē), vai
arī šajā punktā neeksistē vismaz viens no šiem parciālajiem atvasinājumiem
(tas parciālais atvasinājums, kurš eksistē, ir nulle).
ir nulles (protams, ja tie eksistē), vai
arī šajā punktā neeksistē vismaz viens no šiem parciālajiem atvasinājumiem
(tas parciālais atvasinājums, kurš eksistē, ir nulle).
 Pieņem, ka
Pieņem, ka
 ir funkcijas
maksimuma punkts. Tātad šī punkta pārdurtajā apkārtnē izpildās
nevienādība
ir funkcijas
maksimuma punkts. Tātad šī punkta pārdurtajā apkārtnē izpildās
nevienādība
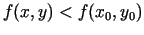 . Izpildās arī nevienādība
. Izpildās arī nevienādība
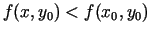 . Tas nozīmē, ka
. Tas nozīmē, ka 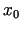 ir funkcijas
ir funkcijas
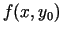 maksimuma punkts. (
maksimuma punkts. (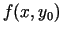 var uzskatīt kā viena
argumenta
var uzskatīt kā viena
argumenta 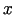 funkciju). Seko, ka šīs funkcijas atvasinājums,
t.i.,
funkciju). Seko, ka šīs funkcijas atvasinājums,
t.i.,
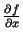 vai nu ir nulle (ja tas
eksistē), vai arī neeksistē. Analoģiski pamato, ka
vai nu ir nulle (ja tas
eksistē), vai arī neeksistē. Analoģiski pamato, ka
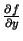 ir vai nu nulle, vai arī neeksistē.
ir vai nu nulle, vai arī neeksistē.
-
4.1. piezīme.
-
 4.1. teorēma ir funkcijas ekstrēma tikai
nepieciešamais nosacījums. Piemēram, funkcijai
4.1. teorēma ir funkcijas ekstrēma tikai
nepieciešamais nosacījums. Piemēram, funkcijai
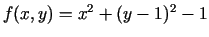 parciālie atvasinājumi
parciālie atvasinājumi
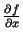 un
un
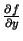 punktā
punktā 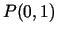 ir nulles, pie tam punkts
ir nulles, pie tam punkts  ir šīs funkcijas
minimuma punkts. Funkcijai
ir šīs funkcijas
minimuma punkts. Funkcijai
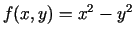 parciālie atvasinājumi
parciālie atvasinājumi
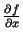 un
un
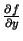 punktā
punktā 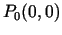 arī ir nulles, bet
arī ir nulles, bet  nav šīs funkcijas
ekstrēma punkts. (Izmantojot ekstrēma punkta definīciju, pamatot
patstāvīgi!).
nav šīs funkcijas
ekstrēma punkts. (Izmantojot ekstrēma punkta definīciju, pamatot
patstāvīgi!).
-
4.2. piezīme.
- Analoģiski definē triju un vairāku mainīgo funkcijas ekstrēma
punktu un ekstrēmu, formulē un pierāda ekstrēma nepieciešamo
nosacījumu.
-
4.2. teorēma.
- (Divu argumentu funkcijas
ekstrēma pietiekamais nosacījums).
Ja funkcijai  punkta
punkta
 apkārtnē
eksistē nepārtraukti pirmās un otrās kārtas parciālie atvasinājumi,
pie tam
apkārtnē
eksistē nepārtraukti pirmās un otrās kārtas parciālie atvasinājumi,
pie tam
un 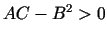 , kur
, kur
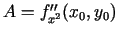 ,
,
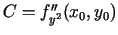 ,
,
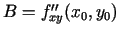 , tad
, tad
 ir šīs
funkcijas ekstrēma punkts. Pie tam
ir šīs
funkcijas ekstrēma punkts. Pie tam
 ir funkcijas maksimuma punkts, ja
ir funkcijas maksimuma punkts, ja
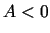 ,
un minimuma punkts, ja
,
un minimuma punkts, ja 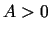 . Ja
. Ja 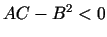 , tad
, tad
 nav šīs funkcijas ekstrēma punkts.
nav šīs funkcijas ekstrēma punkts.
 Funkcijai
Funkcijai  uzraksta Teilora formulu ar
uzraksta Teilora formulu ar
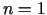 punkta
punkta
 apkārtnē. Argumentu pieaugumus apzīmē ar
apkārtnē. Argumentu pieaugumus apzīmē ar
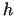 un
un 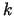 .
.
kur
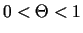 .
.
Tā kā
 ir funkcijas stacionārais punkts, tad
Apzīmē
ir funkcijas stacionārais punkts, tad
Apzīmē
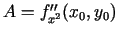 ,
,
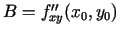 un
un
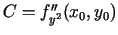 . Saskaņā ar otrās
kārtas parciālo atvasinājumu nepārtrauktību punktā
. Saskaņā ar otrās
kārtas parciālo atvasinājumu nepārtrauktību punktā
 var
rakstīt, ka
var
rakstīt, ka
kur
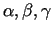 ir bezgalīgi mazas funkcijas, kad
ir bezgalīgi mazas funkcijas, kad
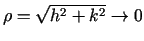 . Teilora formulu var uzrakstīt
šādi:
. Teilora formulu var uzrakstīt
šādi:
No 4.1. zīm. redzams, ka
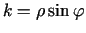 un
un
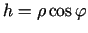 . Tāpēc
. Tāpēc
Apzīmē
(
 - atkarīgi no
- atkarīgi no 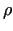 ).
Funkcija
).
Funkcija
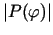 - nepārtraukta intervālā
- nepārtraukta intervālā
![$ [-\pi,\pi]$](img750.gif) , tāpēc tā sasniedz šajā intervālā savu vismazāko
vērtību
, tāpēc tā sasniedz šajā intervālā savu vismazāko
vērtību
![$ m=\min\limits_{[-\pi,\pi]}\left\vert P(\varphi)\right\vert$](img751.gif) .
Tāpēcvisiem
.
Tāpēcvisiem
![$ \varphi~\in~ [-\pi,\pi]$](img752.gif) izpildās
izpildās
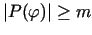 .
.
Funkcijai
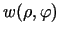 izpildās
izpildās
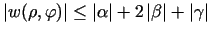 .
Ja
.
Ja
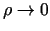 , tad
, tad
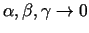 un
un
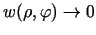 . Tāpēc pietiekoši maziem
. Tāpēc pietiekoši maziem 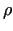 (neatkarīgi no
(neatkarīgi no 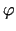 ) izpildās
) izpildās
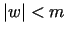 .
.
Punkta
 kaut kādā apkārtnē (pietiekoši mazam
kaut kādā apkārtnē (pietiekoši mazam 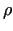 )
izpildās vienlaicīgi
)
izpildās vienlaicīgi
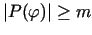 un
un
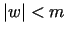 , tāpēc šajā apkārtnē funkcijas pieauguma
, tāpēc šajā apkārtnē funkcijas pieauguma
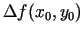 zīmi nosaka
zīmi nosaka
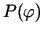 zīme. Konkrēti
zīme. Konkrēti
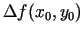 zīme sakrīt ar
zīme sakrīt ar
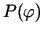 zīmi.
zīmi.
Apskata vairākus gadījumus.
-
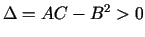 .
.
Pieņem, ka
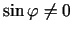 . Tātad
. Tātad
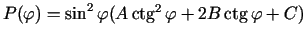 .
Kvadrāttrinoma
.
Kvadrāttrinoma
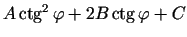 diskriminants ir
tāpēc kvadrāttrinoms, kā arī
diskriminants ir
tāpēc kvadrāttrinoms, kā arī
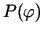 un
un
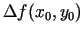 saglabā
saglabā 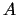 zīmi.
zīmi.
Ja
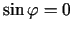 , tad
, tad
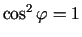 un
un
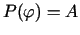 . Arī
šoreiz
. Arī
šoreiz
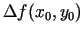 zīme sakrīt ar
zīme sakrīt ar 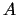 zīmi.
zīmi.
- Ja
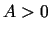 , tad
, tad
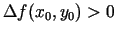 un
un
 -
funkcijas minimuma punkts (skat. 4.1. definīciju);
-
funkcijas minimuma punkts (skat. 4.1. definīciju);
- Ja
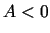 , tad
, tad
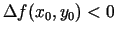 un
un
 -
funkcijas maksimuma punkts.
-
funkcijas maksimuma punkts.
Jāatzīmē, ka šoreiz 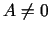 un tā zīme sakrīt ar
un tā zīme sakrīt ar 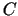 zīmi, jo
pretējā
gadījumā būtu
zīmi, jo
pretējā
gadījumā būtu
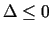 .
.
-
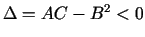 .
.
Pieņem, ka 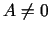 un, piemēram,
un, piemēram, 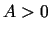 . Tādā gadījumā
Punkta
. Tādā gadījumā
Punkta
 apkārtnē apskata divus virzienus
apkārtnē apskata divus virzienus
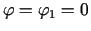 un
un
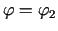 , kur
, kur 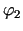 nosaka no vienādojuma
nosaka no vienādojuma
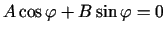 jeb
jeb
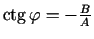 (
(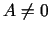 ).
).
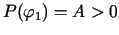 ,
,
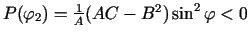 .
.
Punkta
 apkārtnē
apkārtnē
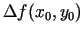 zīmi nesaglabā.
Tādējādi
zīmi nesaglabā.
Tādējādi
 nav funkcijas ekstrēma punkts.
nav funkcijas ekstrēma punkts.
Analoģiski apskata gadījumu, kad 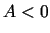 .
.
Beidzot pieņem, ka 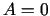 .
.
Iegūst
Šoreiz 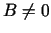 , jo pretējā gadījumā būtu
, jo pretējā gadījumā būtu 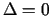 .
.
Izteiksmes
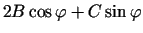 zīme pietiekoši maziem
zīme pietiekoši maziem
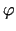 ir atkarīga no
ir atkarīga no
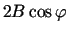 zīmes, jo šādiem
zīmes, jo šādiem 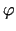 spēkā
spēkā
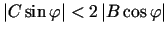 .
.
Starp šādiem 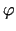 izvēlas
izvēlas 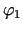 un apskata divus
virzienus
un apskata divus
virzienus
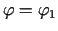 un
un
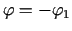 . Acīmredzami
. Acīmredzami
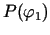 un
un
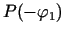 zīmes ir pretējas. Tādējādi
zīmes ir pretējas. Tādējādi
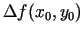 nesaglabā zīmi un
nesaglabā zīmi un
 nav funkcijas ekstrēma
punkts.
nav funkcijas ekstrēma
punkts.
-
4.3. piezīme.
- Ja
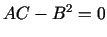 , tad jautājums par punktu
, tad jautājums par punktu
 paliek atklāts.
paliek atklāts.
Funkcijas  pētīšanas uz ekstrēmu shēma.
pētīšanas uz ekstrēmu shēma.
- Atrod
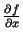 un
un
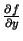 .
.
- Atrod funkcijas stacionāros punktus, t.i., punktus,
kuros
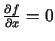 un
un
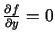 .
.
- Atrod
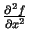 ,
,
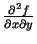 un
un
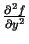 .
.
- Izskaitļo otrās kārtas parciālo atvasinājumu vērtības
stacionārajos punktos, t.i., atrod atbilstošās vērtības
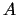 ,
, 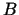 un
un
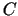 .
.
- Katram stacionāram punktam izskaitļo vērtību
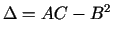 .
.
- Atkarība no
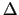 zīmes (nepieciešamības gadījumā arī pēc
zīmes (nepieciešamības gadījumā arī pēc 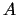 zīmes) izdara secinājumus par punktu
zīmes) izdara secinājumus par punktu
 .
.
-
4.1. piemērs.
- Izpētīt uz ekstrēmu funkciju
Atrod
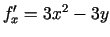 ;
;
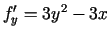 . Atrisina sistēmu
un iegūst funkcijas divus stacionāros punktus
. Atrisina sistēmu
un iegūst funkcijas divus stacionāros punktus  un
un 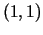 .
Atrod
.
Atrod
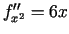 ,
,
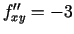 ,
,
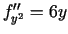 . Katrā no
stacionārajiem punktiem izskaitļo
. Katrā no
stacionārajiem punktiem izskaitļo 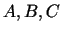 un
un
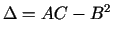 .
.
- Punktā
 :
:
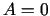 ;
; 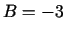 ;
; 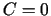 ;
;
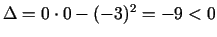 . Punkts
. Punkts  nav funkcijas ekstrēma punkts.
nav funkcijas ekstrēma punkts.
- Punktā
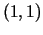 :
:
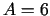 ;
; 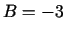 ;
; 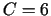 ;
;
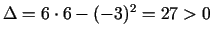 . Punkts
. Punkts 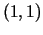 ir funkcijas ekstrēma punkts, pie tam minimuma punkts, jo
ir funkcijas ekstrēma punkts, pie tam minimuma punkts, jo 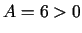 .
Tādējādi
.
Tādējādi
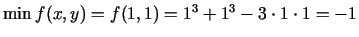 .
.
-
4.4. piezīme.
-
 4.2. teorēma sniedz atbildi tikai par
tiem funkcijas stacionārajiem punktiem, kuros
4.2. teorēma sniedz atbildi tikai par
tiem funkcijas stacionārajiem punktiem, kuros
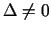 .
Funkcijas tie stacionārie punkti, kuros
.
Funkcijas tie stacionārie punkti, kuros 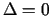 , un punkti, kuros
izpildās ekstrēma nepieciešamais nosacījums, bet kas nav funkcijas
stacionārie punkti, ir jāpēta īpaši. Tam nolūkam var lietot,
piemēram, ekstrēma definīciju.
, un punkti, kuros
izpildās ekstrēma nepieciešamais nosacījums, bet kas nav funkcijas
stacionārie punkti, ir jāpēta īpaši. Tam nolūkam var lietot,
piemēram, ekstrēma definīciju.
-
4.2. piemērs.
- Izpētīt uz ekstrēmu funkciju
Ekstrēma nepieciešamais nosacījums izpildās punktā  . Šajā
punktā funkcija nav diferencējama (
. Šajā
punktā funkcija nav diferencējama (
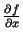 ,
,
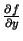 -
neeksistē). Acīmredzami
-
neeksistē). Acīmredzami  ir šīs funkcijas minimuma punkts,
ir šīs funkcijas minimuma punkts,
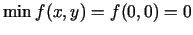 (4.2. zīm.).
(4.2. zīm.).
-
4.3. piemērs.
- Izpētīt uz ekstrēmu funkciju
Atrisina sistēmu
un iegūst funkcijas trīs stacionāros punktus  ,
, 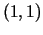 ,
,
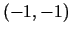 . Atrod
. Atrod
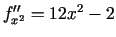 ,
,
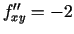 ,
,
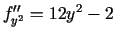 . Katrā no stacionārajiem punktiem izskaitļo
. Katrā no stacionārajiem punktiem izskaitļo  un
un  .
.
Punktā 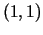 :
:
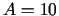 ;
; 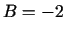 ;
; 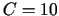 ;
;
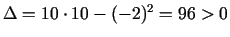 . Punkts
. Punkts
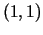 ir funkcijas minimuma punkts,
ir funkcijas minimuma punkts,
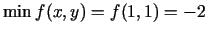 .
Analoģiski punkts
.
Analoģiski punkts 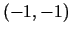 ir arī funkcijas minimuma punkts,
ir arī funkcijas minimuma punkts,
Punktā  :
:
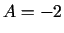 ;
; 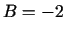 ;
; 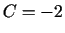 ;
; 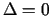 . 4.2. teorēma nav
pielietojama. Ja
. 4.2. teorēma nav
pielietojama. Ja 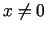 , tad
, tad
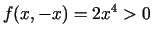 . Ja
. Ja
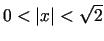 , tad
, tad
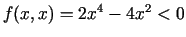 . Punktā
. Punktā  funkcijas vērtība
funkcijas vērtība 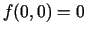 . Tātad punkta
. Tātad punkta  apkārtnē
funkcija var pieņemt gan pozitīvas, gan negatīvas vērtības un
apkārtnē
funkcija var pieņemt gan pozitīvas, gan negatīvas vērtības un
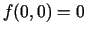 . Tādējādi
. Tādējādi  nav funkcijas ekstrēma punkts.
nav funkcijas ekstrēma punkts.
-
4.4. piemērs.
- Izpētīt uz ekstrēmu funkciju
Atrod
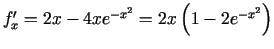 ,
, 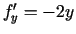 .
Atrisina sistēmu
Funkcijas stacionārie punkti ir
.
Atrisina sistēmu
Funkcijas stacionārie punkti ir  ,
,
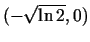 ,
,
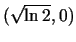 . Atrod
. Atrod
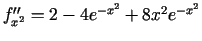 ;
;
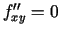 ;
;
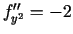 . Atrod
. Atrod  un
un
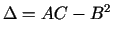 katrā no
stacionārajiem punktiem.
katrā no
stacionārajiem punktiem.
Punktā  :
:
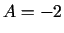 ,
, 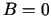 ,
, 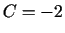 ,
,
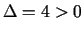 . Tādējādi
. Tādējādi
Punktos
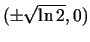 :
:
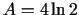 ,
, 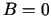 ,
, 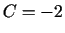 ,
,
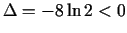 . Tādējādi tie nav
ekstrēma punkti.
. Tādējādi tie nav
ekstrēma punkti.
Punkts  ir funkcijas vienīgais ekstrēma punkts (konkrēti - maksimuma
punkts). Šajā punktā funkcija nesasniedz ne vislielāko, ne
vismazāko vērtību, jo funkcijai
ir funkcijas vienīgais ekstrēma punkts (konkrēti - maksimuma
punkts). Šajā punktā funkcija nesasniedz ne vislielāko, ne
vismazāko vērtību, jo funkcijai
![$ f(0,y)=-y^2+2\xrightarrow[y\rightarrow \infty]{\/} -\infty$](img856.gif) un
funkcijai
un
funkcijai
![$ f(x,0)=x^2+2e^{-x^2}\xrightarrow[x\rightarrow \infty]{\/}
+\infty$](img857.gif) . (Viena argumenta diferencējamai funkcijai vienīgā ekstrēma punkta gadījumā šajā punktā
funkcija sasniedza savu vismazāko vērtību, ja tas bija minimuma punkts un
vislielāko vērtību, ja tas bija maksimuma punkts).
. (Viena argumenta diferencējamai funkcijai vienīgā ekstrēma punkta gadījumā šajā punktā
funkcija sasniedza savu vismazāko vērtību, ja tas bija minimuma punkts un
vislielāko vērtību, ja tas bija maksimuma punkts).
-
4.5. piemērs.
- Izpētīt uz ekstrēmu funkciju
Atrod
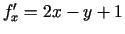 ,
, 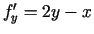 ,
, 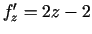 .
Atrisina sistēmu
Punkts
.
Atrisina sistēmu
Punkts
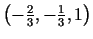 ir vienīgais šīs
funkcijas stacionārais punkts.
ir vienīgais šīs
funkcijas stacionārais punkts.
Ekstrēma pietiekamais nosacījums triju argumentu funkcijai netika
apskatīts. Šoreiz izpēta funkcijas pieauguma zīmi šajā punktā.
(jebkuriem 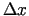 ,
, 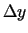 ,
, 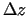 , kas vienlaicīgi nav
nulles). Tādējādi punkts
, kas vienlaicīgi nav
nulles). Tādējādi punkts
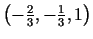 ir funkcijas minimuma punkts.
ir funkcijas minimuma punkts.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 4.2. Divu argumentu funkcijas vismazākās un
Augstāk: 4. VAIRĀKU ARGUMENTU FUNKCIJU PĒTĪŠANA UZ
Iepriekšējais: 4. VAIRĀKU ARGUMENTU FUNKCIJU PĒTĪŠANA UZ
2002-06-21
![]() apkārtnē definētu funkciju
apkārtnē definētu funkciju ![]() ,
kas nepārtraukta šajā punktā.
,
kas nepārtraukta šajā punktā.
![]() punkts
punkts ![]() ir tās
minimuma punkts un
ir tās
minimuma punkts un
![]() .
.
![]() ir funkcijas
ir funkcijas ![]() ekstrēma punkts, tad
šajā
punktā funkcijas parciālie atvasinājumi
ekstrēma punkts, tad
šajā
punktā funkcijas parciālie atvasinājumi
![]() un
un
![]() ir nulles (protams, ja tie eksistē), vai
arī šajā punktā neeksistē vismaz viens no šiem parciālajiem atvasinājumiem
(tas parciālais atvasinājums, kurš eksistē, ir nulle).
ir nulles (protams, ja tie eksistē), vai
arī šajā punktā neeksistē vismaz viens no šiem parciālajiem atvasinājumiem
(tas parciālais atvasinājums, kurš eksistē, ir nulle).
![]() Pieņem, ka
Pieņem, ka
![]() ir funkcijas
maksimuma punkts. Tātad šī punkta pārdurtajā apkārtnē izpildās
nevienādība
ir funkcijas
maksimuma punkts. Tātad šī punkta pārdurtajā apkārtnē izpildās
nevienādība
![]() . Izpildās arī nevienādība
. Izpildās arī nevienādība
![]() . Tas nozīmē, ka
. Tas nozīmē, ka ![]() ir funkcijas
ir funkcijas
![]() maksimuma punkts. (
maksimuma punkts. (![]() var uzskatīt kā viena
argumenta
var uzskatīt kā viena
argumenta ![]() funkciju). Seko, ka šīs funkcijas atvasinājums,
t.i.,
funkciju). Seko, ka šīs funkcijas atvasinājums,
t.i.,
![]() vai nu ir nulle (ja tas
eksistē), vai arī neeksistē. Analoģiski pamato, ka
vai nu ir nulle (ja tas
eksistē), vai arī neeksistē. Analoģiski pamato, ka
![]() ir vai nu nulle, vai arī neeksistē.
ir vai nu nulle, vai arī neeksistē.
![]()
![]() punkta
punkta
![]() apkārtnē
eksistē nepārtraukti pirmās un otrās kārtas parciālie atvasinājumi,
pie tam
apkārtnē
eksistē nepārtraukti pirmās un otrās kārtas parciālie atvasinājumi,
pie tam
![]() Funkcijai
Funkcijai ![]() uzraksta Teilora formulu ar
uzraksta Teilora formulu ar
![]() punkta
punkta
![]() apkārtnē. Argumentu pieaugumus apzīmē ar
apkārtnē. Argumentu pieaugumus apzīmē ar
![]() un
un ![]() .
.
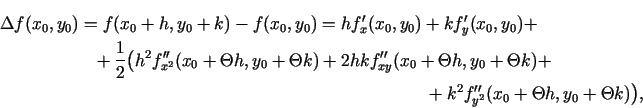
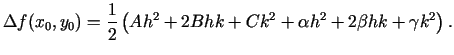
![]() un
un
![]() . Tāpēc
. Tāpēc
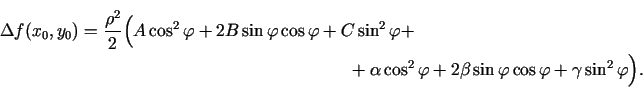
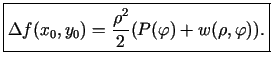
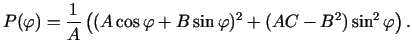
![]() pētīšanas uz ekstrēmu shēma.
pētīšanas uz ekstrēmu shēma.
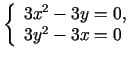
![]() ;
; ![]() ;
; ![]() ;
;
![]() . Punkts
. Punkts ![]() nav funkcijas ekstrēma punkts.
nav funkcijas ekstrēma punkts.
![]() ;
; ![]() ;
; ![]() ;
;
![]() . Punkts
. Punkts ![]() ir funkcijas ekstrēma punkts, pie tam minimuma punkts, jo
ir funkcijas ekstrēma punkts, pie tam minimuma punkts, jo ![]() .
Tādējādi
.
Tādējādi
![]() .
.
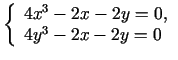
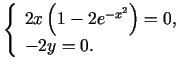
![]() :
:
![]() ,
, ![]() ,
, ![]() ,
,
![]() . Tādējādi tie nav
ekstrēma punkti.
. Tādējādi tie nav
ekstrēma punkti.