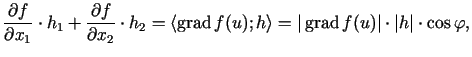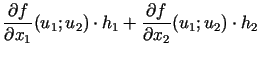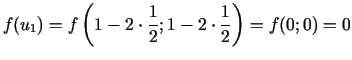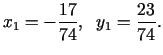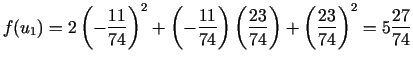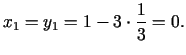Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.3.2. Šķēlumu metode
Augstāk: 2.3. Minimuma punkta meklēšanas metodes vairāku
Iepriekšējais: 2.3. Minimuma punkta meklēšanas metodes vairāku
Aplūkosim funkciju
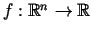 , kurai
eksistē nepārtraukti pirmās kārtas parciālie atvasinājumi. Par
funkcijas gradientu sauc vektoru
, kurai
eksistē nepārtraukti pirmās kārtas parciālie atvasinājumi. Par
funkcijas gradientu sauc vektoru
No matemātiskas analīzes kursa ir zināms [3, 184. lpp.], ka
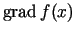 ir vektors, kas vērsts funkcijas straujākās augšanas
virzienā.
ir vektors, kas vērsts funkcijas straujākās augšanas
virzienā.
Piemēram, aplūkosim divu argumentu
funkciju
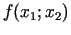 un tās pieaugumu punktā
un tās pieaugumu punktā
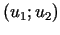 :
:
kur 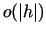 ir augstākas kārtas loceklis nekā
ir augstākas kārtas loceklis nekā
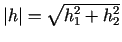 , t.i.,
, t.i.,
Ir spēkā formula
kur 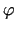 ir leņķis starp vektoriem
ir leņķis starp vektoriem
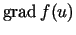 un
un
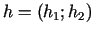 . Pieņemsim, ka vektors
. Pieņemsim, ka vektors
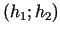 ir
normēts, t.i.,
ir
normēts, t.i.,
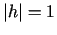 . Viegli redzēt, ka summa
. Viegli redzēt, ka summa
būs vislielākā tad, kad pieauguma vektors
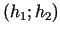 ir
vērsts funkcijas
ir
vērsts funkcijas  gradienta virzienā (t.i., vektori
gradienta virzienā (t.i., vektori
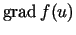 un
un
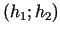 ir kolineāri), jo tad
ir kolineāri), jo tad
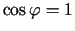 .
.
-
2.1. piezīme.
- Atzīmēsim, ka vektors
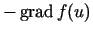 , kuru sauc
par antigradientu, ir vērsts funkcijas straujākās
dilšanas virzienā.
, kuru sauc
par antigradientu, ir vērsts funkcijas straujākās
dilšanas virzienā.
-
2.5. piemērs.
- Funkcijas
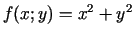 , kuras grafiks ir eliptiskais
paraboloīds ar virsotni koordinātu sākumpunktā,
antigradienta vektors
, kuras grafiks ir eliptiskais
paraboloīds ar virsotni koordinātu sākumpunktā,
antigradienta vektors 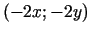 jebkurā nenulles punktā
jebkurā nenulles punktā 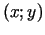 ir vērsts uz koordinātu sākumpunktu.
ir vērsts uz koordinātu sākumpunktu.
Gradientu metodes centrālā ideja - virzīties uz funkcijas
iespējamo minimuma punktu pa lauztu līniju tā, lai katrā lūzuma
punktā kustības virziens sakristu ar antigradienta
virzienu.
Gradientu metodes iteratīva
formula:
kur
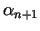 - pozitīvs skaitlis.
- pozitīvs skaitlis.
Parametra 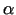 izvēle. Katrā solī ir jāizvēlas
parametra
izvēle. Katrā solī ir jāizvēlas
parametra 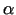 vērtība. Ja skaitļa
vērtība. Ja skaitļa 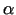 vērtība ir pārāk
liela, tad funkcijas
vērtība ir pārāk
liela, tad funkcijas  vērtība punktā
vērtība punktā 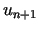 var kļūt lielāka
par
var kļūt lielāka
par 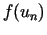 .
.
-
2.6. piemērs.
- Apskatīsim problēmu
Pieņemsim, ka sākumpunkts ir
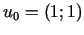 . Tad
. Tad
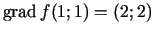 . Ja
. Ja
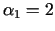 , tad tuvinājums
, tad tuvinājums
Acīmredzot,
Var arī gadīties, ka process kļūs oscilējošs. Tā, pieņemsim, ka
iepriekšējā piemērā
Tad
Katrā solī parametrs 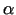 ir jāizvēlās tā, lai funkcijas
ir jāizvēlās tā, lai funkcijas  vērtība punktā
vērtība punktā
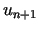 būtu pēc iespējas mazāka. Meklējam
būtu pēc iespējas mazāka. Meklējam
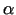 kā viena argumenta funkcijas minimizēšanas problēmas
kā viena argumenta funkcijas minimizēšanas problēmas
atrisinājumu.
-
2.7. piemērs.
- Apskatīsim problēmu
Pieņemsim, ka sākumpunkts ir
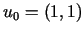 . Tad
. Tad
kur
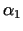 ir problēmas
ir problēmas
atrisinājums. Funkcijas
minimuma punkts ir
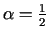 . Tad
. Tad
un funkcijas  minimums (un minimuma punkts) ir atrasts jau
pirmajā solī.
minimums (un minimuma punkts) ir atrasts jau
pirmajā solī.
-
2.8. piemērs.
- Apskatīsim problēmu
Funkcijas  gradients
gradients
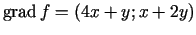 . Pieņemsim, ka
sākumpunkts ir
. Pieņemsim, ka
sākumpunkts ir
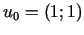 .
.
Pirmajā solī
no kurienes izriet
Meklējam optimālo
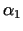 , risinot minimizēšanas problēmu
, risinot minimizēšanas problēmu
Pēc
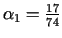 atrašanas aprēķinām
atrašanas aprēķinām
Atrodam
un aprēķinus var turpināt tālāk.
-
2.9. piemērs.
- Apskatīsim problēmu
Funkcijas  gradients
gradients
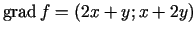 . Pieņemsim, ka
sākumpunkts ir
. Pieņemsim, ka
sākumpunkts ir
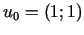 .
.
Pirmajā solī
no kurienes izriet
Meklējam optimālo 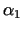 , risinot minimizēšanas problēmu
, risinot minimizēšanas problēmu
Pēc
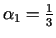 atrašanas aprēķinām
atrašanas aprēķinām
Atrodam
un, acīmredzot, tā ir funkcijas  minimālā vērtība.
minimālā vērtība.
-
2.2. piezīme.
- Gadījumos, kad antigradienta vektors
sākumpunktā
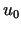 ir vērsts uz minimuma punktu, gradientu metode
dod precīzu atbildi jau pirmajā solī.
ir vērsts uz minimuma punktu, gradientu metode
dod precīzu atbildi jau pirmajā solī.
-
2.3. piezīme.
- Izvērstāku informāciju par gradientu metodi var
iegūt grāmatās [1], [3], [5].



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.3.2. Šķēlumu metode
Augstāk: 2.3. Minimuma punkta meklēšanas metodes vairāku
Iepriekšējais: 2.3. Minimuma punkta meklēšanas metodes vairāku
2002-05-04
![]() , kurai
eksistē nepārtraukti pirmās kārtas parciālie atvasinājumi. Par
funkcijas gradientu sauc vektoru
, kurai
eksistē nepārtraukti pirmās kārtas parciālie atvasinājumi. Par
funkcijas gradientu sauc vektoru
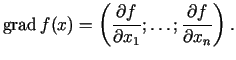
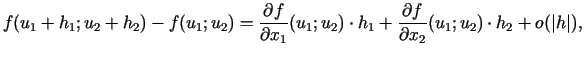
![$\displaystyle \frac{o(\vert h\vert)}{\vert h\vert}\xrightarrow[{\vert h\vert\to 0}]{}0.$](img627.gif)