1. No nogriežņa ![]() izmet vaļēju intervālu
izmet vaļēju intervālu
![]() ; no pāri palikušajiem
nogriežņiem izmet divus vaļējus intervālus ar centriem šo
nogriežņu viduspunktos un kopējo garumu
; no pāri palikušajiem
nogriežņiem izmet divus vaļējus intervālus ar centriem šo
nogriežņu viduspunktos un kopējo garumu
![]() ; no pāri
palikušajiem nogriežņiem izmet četrus vaļējus intervālus ar
centriem šo nogriežņu viduspunktos un kopējo garumu
; no pāri
palikušajiem nogriežņiem izmet četrus vaļējus intervālus ar
centriem šo nogriežņu viduspunktos un kopējo garumu
![]() u.t.t. Ar
u.t.t. Ar ![]() apzīmēsim kopu, kas paliek pāri no nogriežņa
apzīmēsim kopu, kas paliek pāri no nogriežņa
![]() , bezgalīgi turpinot šo konstrukciju. Pierādīt, ka kopa
, bezgalīgi turpinot šo konstrukciju. Pierādīt, ka kopa
![]() ir mērojama Lebega nozīmē un atrast tās Lebega mēru.
ir mērojama Lebega nozīmē un atrast tās Lebega mēru.
2. Vai funkcija ![]() ir integrējama Rīmaņa nozīmē kopā
ir integrējama Rīmaņa nozīmē kopā
![]() ? Vai funkcija
? Vai funkcija ![]() ir integrējama Lebega nozīmē
kopā
ir integrējama Lebega nozīmē
kopā ![]() ? Aprēķināt funkcijas
? Aprēķināt funkcijas ![]() integrāli (Rīmaņa vai
Lebega) kopā
integrāli (Rīmaņa vai
Lebega) kopā ![]() .
.
 |
3. Aprēķināt funkcijas ![]() Lebega integrāli
kopā
Lebega integrāli
kopā ![]() . Vai funkcija
. Vai funkcija ![]() ir summējama kopā
ir summējama kopā
![]() ?
?
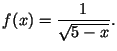 |