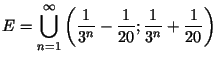 |
1. Pierādīt, ka kopa
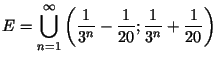 |
2. Vai funkcija ![]() ir integrējama Rīmaņa nozīmē kopā
ir integrējama Rīmaņa nozīmē kopā
![]() ? Vai funkcija
? Vai funkcija ![]() ir integrējama Lebega nozīmē
kopā
ir integrējama Lebega nozīmē
kopā ![]() ? Aprēķināt funkcijas
? Aprēķināt funkcijas ![]() integrāli (Rīmaņa vai
Lebega) kopā
integrāli (Rīmaņa vai
Lebega) kopā ![]() .
.
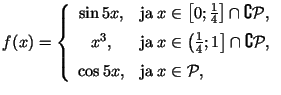 |
3. Aprēķināt funkcijas ![]() Lebega integrāli
kopā
Lebega integrāli
kopā ![]() . Vai funkcija
. Vai funkcija ![]() ir summējama kopā
ir summējama kopā
![]() ?
?
![$\displaystyle f(x)=\left\{\begin{array}{ccl} 10x^2\/, & \text{ja} & x\in \mathc...
...t[7]{x}}\/, & \text{ja} & x\in[0;1]\setminus\mathcal{P}\/, \ \end{array}\right.$](img63.gif) |