1. Apskatīsim kopas ![]() apakškopu
apakškopu ![]() , kas sastāv no visiem
tiem skaitļiem, kuri var tikt izteikti
, kas sastāv no visiem
tiem skaitļiem, kuri var tikt izteikti ![]() skaitīšanas sistēmā,
pēc komata neizmantojot ciparus 0 un
skaitīšanas sistēmā,
pēc komata neizmantojot ciparus 0 un ![]() . Pierādīt, ka kopa
. Pierādīt, ka kopa ![]() ir mērojama Lebega nozīmē un atrast tās Lebega
mēru.
ir mērojama Lebega nozīmē un atrast tās Lebega
mēru.
2. Vai funkcija ![]() ir
integrējama Rīmaņa nozīmē kopā
ir
integrējama Rīmaņa nozīmē kopā ![]() ? Vai funkcija
? Vai funkcija
![]() ir integrējama Lebega nozīmē kopā
ir integrējama Lebega nozīmē kopā ![]() ?
Aprēķināt funkcijas
?
Aprēķināt funkcijas ![]() integrāli (Rīmaņa vai Lebega) kopā
integrāli (Rīmaņa vai Lebega) kopā
![]() .
.
![$\displaystyle f(x)=\left\{\begin{array}{cl} x^2+1\/,&{\rm ja}\;x\in \left[0;\fr...
...\smallskip\\ 5^{x}\/,&{\rm ja}\;x\in [0;1]\cap\mathbb{Q}\/, \end{array}\right.$](img56.gif) |
3. Aprēķināt funkcijas ![]() Lebega integrāli
kopā
Lebega integrāli
kopā ![]() . Vai funkcija
. Vai funkcija ![]() ir summējama kopā
ir summējama kopā
![]() ?
?
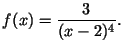 |