


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 5. PIELIKUMS
Augstāk: 4. VAIRĀKU ARGUMENTU FUNKCIJU PĒTĪŠANA UZ
Iepriekšējais: 4.3. Jautājumi
- Formulēt un pierādīt ekstrēma nepieciešamo nosacījumu triju
argumentu funkcijai.
- Atrast funkcijas
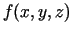 gradientu tās stacionārajā
punktā.
gradientu tās stacionārajā
punktā.
- Uzrakstīt pieskares vienādojumu diferencējamas funkcijas
 grafikam punktā
grafikam punktā
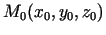 , kur
, kur
 šīs
funkcijas ekstrēma
šīs
funkcijas ekstrēma
punkts.
- Izmantojot definīciju, pierādīt, ka funkcijai
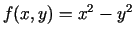 punkts
punkts  nav ekstrēma punkts.
nav ekstrēma punkts.
- Izmantojot definīciju un izmantojot ekstrēma pietiekamo
nosacījumu, pierādīt, ka funkcijai
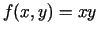 punkts
punkts  nav
ekstrēma punkts.
nav
ekstrēma punkts.
- Izpētīt uz ekstrēmu funkcijas:
a)
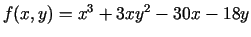 ;
;
b)
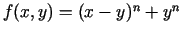 , kur
, kur 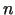 - naturāls skaitlis, kurš lielāks
par
- naturāls skaitlis, kurš lielāks
par 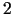 .
.
- Parādīt, ka funkcijai
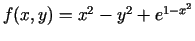 eksistē
vienīgais ekstrēma punkts, bet šajā punktā funkcija nesasniedz ne
vismazāko, ne vislielāko vērtību.
eksistē
vienīgais ekstrēma punkts, bet šajā punktā funkcija nesasniedz ne
vismazāko, ne vislielāko vērtību.
- Paskaidrot, kā pēta uz ekstrēmu triju argumentu
funkciju.
- Atrast funkcijas
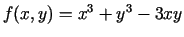 vismazāko un vislielāko
vērtību kopā
vismazāko un vislielāko
vērtību kopā  , kuru ierobežo taisnes
, kuru ierobežo taisnes 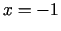 ,
, 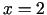 ,
, 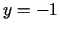 ,
,
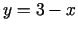 .
.
- Atrast funkcijas
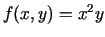 vislielāko un vismazāko
vērtību kopā
vislielāko un vismazāko
vērtību kopā  , kuru ierobežo parabola
, kuru ierobežo parabola 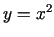 un taisne
un taisne 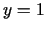 .
.
- Atrast funkcijas
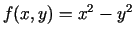 vismazāko un vislielāko
vērtību kopā, kuru nosaka nevienādība
vismazāko un vislielāko
vērtību kopā, kuru nosaka nevienādība
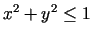 .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 5. PIELIKUMS
Augstāk: 4. VAIRĀKU ARGUMENTU FUNKCIJU PĒTĪŠANA UZ
Iepriekšējais: 4.3. Jautājumi
2002-06-21