


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.2. Vairāku argumentu funkcijas ģeometriskā interpretācija
Augstāk: 1. PAMATJĒDZIENI
Iepriekšējais: 1. PAMATJĒDZIENI
Apskata kopu  , kuras elementi ir reālo skaitļu
sakārtoti pāri
, kuras elementi ir reālo skaitļu
sakārtoti pāri 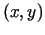 . Katram kopas
. Katram kopas  elementam
elementam 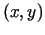 tiek
piekārtots noteikts reāls skaitlis. Šādos gadījumos saka, ka kopā
tiek
piekārtots noteikts reāls skaitlis. Šādos gadījumos saka, ka kopā
 ir definēta divu argumentu
ir definēta divu argumentu 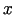 un
un 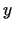 funkcija
funkcija 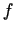 . Funkcijas
. Funkcijas
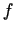 vērtību punktā
vērtību punktā 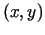 apzīmē ar
apzīmē ar  1.1. Kopu
1.1. Kopu  sauc par funkcijas
sauc par funkcijas
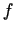 definīcijas apgabalu, bet visu tās
vērtību (ko tā iegūst kopā
definīcijas apgabalu, bet visu tās
vērtību (ko tā iegūst kopā  ) kopu sauc par funkcijas
) kopu sauc par funkcijas
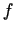 vērtību apgabalu.
vērtību apgabalu.
-
1.1. piezīme.
- Analoģiski rīkojoties, var apskatīt triju argumentu
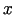 ,
,
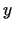 un
un 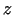 funkciju
funkciju
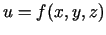 . Šoreiz kopu
. Šoreiz kopu  veido reālo
skaitļu sakārtotas trijotnes
veido reālo
skaitļu sakārtotas trijotnes 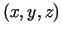 . Visbeidzot var apskatīt
. Visbeidzot var apskatīt
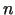 argumentu
argumentu
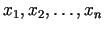 funkciju
funkciju
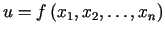 . Visas apskatītās funkcijas sauc par
vairāku argumentu funkcijām.
. Visas apskatītās funkcijas sauc par
vairāku argumentu funkcijām.
Ja apzīmē ar 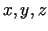 taisnstūra paralēlskaldņa malu
garumus, tad paralēlskaldņa tilpums
taisnstūra paralēlskaldņa malu
garumus, tad paralēlskaldņa tilpums 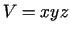 ir triju
argumentu funkcija.
ir triju
argumentu funkcija.
Lai uzdotu funkciju, ir jānorāda kopa  un piekārtošanas likums
saskaņā ar kuru katram šīs kopas elementam (punktam) tiek piekārtots
noteikts reāls skaitlis.
un piekārtošanas likums
saskaņā ar kuru katram šīs kopas elementam (punktam) tiek piekārtots
noteikts reāls skaitlis.
Tāpat kā viena argumenta funkcijas, vairāku argumentu funkcijas
visbiežāk uzdod analītiski, t.i., ar formulu. Ja funkcija ir
uzdota analītiski, tad parasti tās definīcijas apgabalu īpaši
nenorāda, bet ar  saprot pāru
saprot pāru 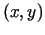 (divu argumentu
funkcijai), trijotņu
(divu argumentu
funkcijai), trijotņu 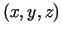 (triju argumentu funkcijai) utt.
kopu, ar kuras elementiem formulai ir jēga.
(triju argumentu funkcijai) utt.
kopu, ar kuras elementiem formulai ir jēga.
Piemēram, funkcijas
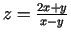 definīcijas apgabals ir
divas pusplaknes, kas atrodas zem un virs taisnes
definīcijas apgabals ir
divas pusplaknes, kas atrodas zem un virs taisnes 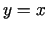 . Funkcijai
. Funkcijai
![$ z=\sqrt[4]{1-x^2-y^2}$](img33.gif) par
par  ir riņķis
ir riņķis
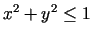 .
Visbeidzot funkcijai
.
Visbeidzot funkcijai
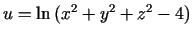 par
par  ir
kopa, kuras elementi
ir
kopa, kuras elementi 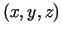 apmierina nevienādību
apmierina nevienādību
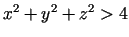 . Pēdējā gadījumā kopu
. Pēdējā gadījumā kopu  veido telpas tie punkti,
kas atrodas ārpus sfēras ar centru punktā
veido telpas tie punkti,
kas atrodas ārpus sfēras ar centru punktā 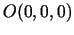 un rādiusu
un rādiusu
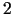 .
.
-
1.2. piezīme.
- Par divu argumentu funkcijas definīcijas apgabalu ir
plaknes kaut kāda apakškopa, bet par triju argumentu funkcijas
definīcijas apgabalu ir telpas apakškopa.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 1.2. Vairāku argumentu funkcijas ģeometriskā interpretācija
Augstāk: 1. PAMATJĒDZIENI
Iepriekšējais: 1. PAMATJĒDZIENI
2002-06-21
![]() , kuras elementi ir reālo skaitļu
sakārtoti pāri
, kuras elementi ir reālo skaitļu
sakārtoti pāri ![]() . Katram kopas
. Katram kopas ![]() elementam
elementam ![]() tiek
piekārtots noteikts reāls skaitlis. Šādos gadījumos saka, ka kopā
tiek
piekārtots noteikts reāls skaitlis. Šādos gadījumos saka, ka kopā
![]() ir definēta divu argumentu
ir definēta divu argumentu ![]() un
un ![]() funkcija
funkcija ![]() . Funkcijas
. Funkcijas
![]() vērtību punktā
vērtību punktā ![]() apzīmē ar
apzīmē ar ![]() 1.1. Kopu
1.1. Kopu ![]() sauc par funkcijas
sauc par funkcijas
![]() definīcijas apgabalu, bet visu tās
vērtību (ko tā iegūst kopā
definīcijas apgabalu, bet visu tās
vērtību (ko tā iegūst kopā ![]() ) kopu sauc par funkcijas
) kopu sauc par funkcijas
![]() vērtību apgabalu.
vērtību apgabalu.
![]() taisnstūra paralēlskaldņa malu
garumus, tad paralēlskaldņa tilpums
taisnstūra paralēlskaldņa malu
garumus, tad paralēlskaldņa tilpums ![]() ir triju
argumentu funkcija.
ir triju
argumentu funkcija.