


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3. ATVASINĀJUMA LIETOJUMI FUNKCIJU PĒTĪŠANĀ
Augstāk: 2. DIFERENCIĀLRĒĶINU PAMATTEORĒMAS
Iepriekšējais: 2.7. Jautājumi
- Pierādīt Fermā teorēmu gadījumā, kad
punktā
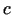 funkcija sasniedz savu vismazāko vērtību. Sniegt ģ
eometrisko interpretāciju.
funkcija sasniedz savu vismazāko vērtību. Sniegt ģ
eometrisko interpretāciju.
- Ar konkrētiem piemēriem parādīt, ka visi Rolla
teorēmas nosacījumi ir būtiski.
- Ar konkrētiem piemēriem parādīt, ka visi
Lagranža teorēmas nosacījumi ir būtiski.
- Šādām funkcijām uzrakstīt Lagranža
formulu:
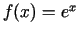 ;
;
-
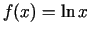 ;
;
-
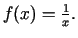
- Pierādīt Košī teorēmu par funkciju
diferenču attiecību.
- Parādīt, ka Lagranža teorēma ir Košī teorēmas secinājums.
- Pierādīt, ka Lopitāla teorēma ir
spēkā, ja
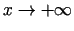 vai
vai
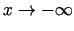 .
.
- Izmantojot Lopitāla kārtulu, aprēķināt
šādas robežas:
-
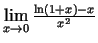 ;
;
-
![$ \lim\limits_{x\rightarrow +\infty}\frac{\ln x}{\sqrt[3]{x}}$](img608.gif) ;
;
-
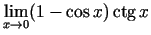 ;
;
-
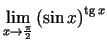 ;
;
-
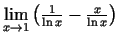 ;
;
-
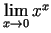 ;
;
-
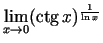 .
.
- Iegūt Teilora formulu
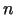 - tās pakāpes polinomam.
- tās pakāpes polinomam.
- Parādīt, ka Teilora formulas atlikuma loceklis ir
augstākās kārtas bezgalīgi maza funkcija salīdzinājumā ar
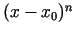 , kad
, kad
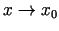 .
.
- Iegūt Teilora formulas atlikuma locekļa Košī formu.
- Šādām funkcijām uzrakstīt Teilora formulu
pēc
 pakāpēm ar atlikuma locekli Lagranža formā:
pakāpēm ar atlikuma locekli Lagranža formā:
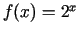 ;
;
-
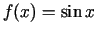 ;
;
-
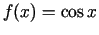 ;
;
-
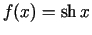 ;
;
-
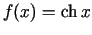 ;
;
-
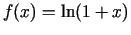 ;
;
-
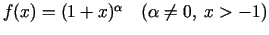 .
.
- Šādām funkcijām uzrakstīt Teilora
formulu pēc
 pakāpēm ar atlikuma locekli Košī formā:
pakāpēm ar atlikuma locekli Košī formā:
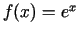 ;
;
-
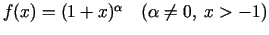 .
.
- Aprēķināt ar precizitāti
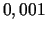 skaitli
skaitli 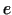 .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 3. ATVASINĀJUMA LIETOJUMI FUNKCIJU PĒTĪŠANĀ
Augstāk: 2. DIFERENCIĀLRĒĶINU PAMATTEORĒMAS
Iepriekšējais: 2.7. Jautājumi
2002-01-21
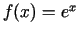 ;
;
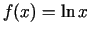 ;
;
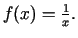
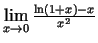 ;
;
![$ \lim\limits_{x\rightarrow +\infty}\frac{\ln x}{\sqrt[3]{x}}$](img608.gif) ;
;
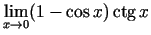 ;
;
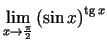 ;
;
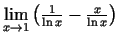 ;
;
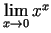 ;
;
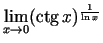 .
.
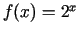 ;
;
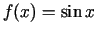 ;
;
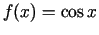 ;
;
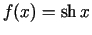 ;
;
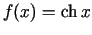 ;
;
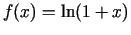 ;
;
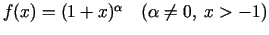 .
.
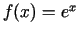 ;
;
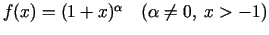 .
.