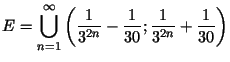 |
1. Pierādīt, ka kopa
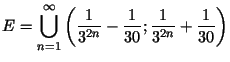 |
2. Vai funkcija ![]() ir integrējama Rīmaņa nozīmē kopā
ir integrējama Rīmaņa nozīmē kopā
![]() ? Vai funkcija
? Vai funkcija ![]() ir integrējama Lebega nozīmē
kopā
ir integrējama Lebega nozīmē
kopā ![]() ? Aprēķināt funkcijas
? Aprēķināt funkcijas ![]() integrāli (Rīmaņa vai
Lebega) kopā
integrāli (Rīmaņa vai
Lebega) kopā ![]() .
.
Funkcija ![]() ir definēta šādi:
Kantora kopas punktos funkcijas
ir definēta šādi:
Kantora kopas punktos funkcijas ![]() v
v![]() rt
rt![]() ba ir
vien
ba ir
vien![]() da ar 0, Kantora kopas blakusinterv
da ar 0, Kantora kopas blakusinterv![]() lu viduspunktos
funkcijas
lu viduspunktos
funkcijas ![]() v
v![]() rt
rt![]() ba ir vien
ba ir vien![]() da ar
da ar
![]() ,
bet uz nogrie
,
bet uz nogrie![]()
![]() iem
iem
![]() un
un
![]() funkcija
funkcija ![]() ir
line
ir
line![]() ra, kur Kantora kopas blakusinterv
ra, kur Kantora kopas blakusinterv![]() li
li ![]() ir
sanumur
ir
sanumur![]() ti š
ti š![]() di:
di:
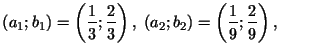
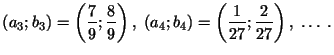
3. Aprēķināt funkcijas ![]() Lebega integrāli
kopā
Lebega integrāli
kopā ![]() . Vai funkcija
. Vai funkcija ![]() ir summējama kopā
ir summējama kopā
![]() ?
?
![$\displaystyle f(x)=\frac{1}{\sqrt[5]{x-1}}\/.$](img91.gif) |