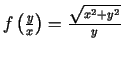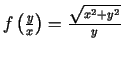Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2. VAIRĀKU ARGUMENTU FUNKCIJAS ROBEŽA UN
Augstāk: 1. PAMATJĒDZIENI
Iepriekšējais: 1.3. Jautājumi
- Izteikt konusa tilpumu
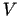 kā veidules
kā veidules 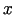 un pamata rādiusa
un pamata rādiusa
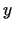 funkciju.
funkciju.
-
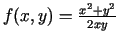 . Atrast
. Atrast 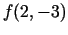 ,
,
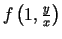 .
.
-
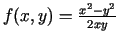 . Atrast
. Atrast 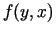 ,
, 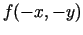 ,
,
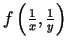 ,
,
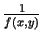 .
.
- Atrast funkcijas
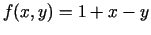 vērtības parabolas
vērtības parabolas 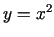 punktos un konstruēt funkcijas
punktos un konstruēt funkcijas
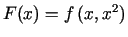 grafiku.
grafiku.
- Atrast
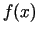 , ja
, ja
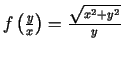
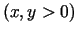 .
.
- Atrast funkcijas
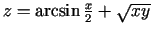 definīcijas
apgabalu un attēlot to koordinātu plaknē.
definīcijas
apgabalu un attēlot to koordinātu plaknē.
- Atrast funkcijas
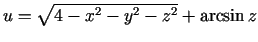 definīcijas apgabalu un sniegt tam ģeometrisko interpretāciju.
definīcijas apgabalu un sniegt tam ģeometrisko interpretāciju.
- Konstruēt līmeņlīnijas funkcijai
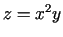 un attēlot tās
koordinātu plaknē.
un attēlot tās
koordinātu plaknē.
- Konstruēt līmeņlīnijas funkcijai
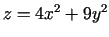 un attēlot tās
koordinātu plaknē. Sniegt ģeometrisko interpretāciju dotās
funkcijas grafikam.
un attēlot tās
koordinātu plaknē. Sniegt ģeometrisko interpretāciju dotās
funkcijas grafikam.
- Konstruēt līmeņvirsmas funkcijai
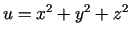 un sniegt
tām ģeometrisko interpretāciju.
un sniegt
tām ģeometrisko interpretāciju.
- Noskaidrot, kuras no funkcijām ierobežotas no augšas,
ierobežotas no apakšas, ierobežotas:
a)
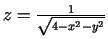 ;
;
b)
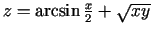 ;
;
c)
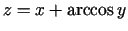 ;
;
d)
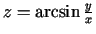 ;
;
e)
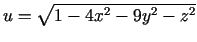 .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2. VAIRĀKU ARGUMENTU FUNKCIJAS ROBEŽA UN
Augstāk: 1. PAMATJĒDZIENI
Iepriekšējais: 1.3. Jautājumi
2002-06-21