


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 5.1.1. Jautājumi
Augstāk: 5. PIELIKUMS
Iepriekšējais: 5. PIELIKUMS
Kā zināms, vienādojums 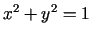 plaknē nosaka vienības riņķa
līniju ar centru koordinātu sākuma punktā. Šis pats vienādojums telpā
nosaka cilindrisku virsmu ar veiduli, kas ir paralēla aplikātu asij.
plaknē nosaka vienības riņķa
līniju ar centru koordinātu sākuma punktā. Šis pats vienādojums telpā
nosaka cilindrisku virsmu ar veiduli, kas ir paralēla aplikātu asij.
Vispārīgi, vienādojums
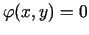 plaknē nosaka kaut kādu
līniju, bet telpā - cilindrisku virsmu. Funkcija
plaknē nosaka kaut kādu
līniju, bet telpā - cilindrisku virsmu. Funkcija  telpā
nosaka kaut kādu virsmu
telpā
nosaka kaut kādu virsmu  , kas šķeļas ar cilindrisku virsmu
, kas šķeļas ar cilindrisku virsmu
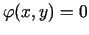 pa telpisku līniju. Uz šīs līnijas telpā var būt
minimuma un maksimuma punkti, kurus sauc par nosacītā
ekstrēma punktiem.
pa telpisku līniju. Uz šīs līnijas telpā var būt
minimuma un maksimuma punkti, kurus sauc par nosacītā
ekstrēma punktiem.
Izvēlas punktu  , kas apmierina vienādojumu
, kas apmierina vienādojumu
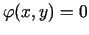 un apskata šī punkta apkārtnē definētu funkciju
un apskata šī punkta apkārtnē definētu funkciju
 , kas ir nepārtraukta punktā
, kas ir nepārtraukta punktā  .
.
-
5.1. definīcija.
- Ja visiem
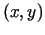 , kas apmierina
vienādojumu
, kas apmierina
vienādojumu
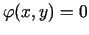 un pieder punkta
un pieder punkta  pārdurtai
apkārtnei, izpildās nevienādība
pārdurtai
apkārtnei, izpildās nevienādība
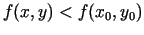 , tad
, tad  sauc funkcijas
sauc funkcijas  nosacītā maksimuma punktu.
Vienādojumu
nosacītā maksimuma punktu.
Vienādojumu
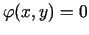 sauc par saites vienādojumu.
sauc par saites vienādojumu.
Analoģiski definē funkcijas  nosacītā minimuma punktu.
nosacītā minimuma punktu.
-
5.1. piezīme.
- Funkcijas
 nosacītā maksimuma punkta definīcija
ir līdzīga tās maksimuma punkta definīcijai. Atšķirība ir tikai
tā, ka no
nosacītā maksimuma punkta definīcija
ir līdzīga tās maksimuma punkta definīcijai. Atšķirība ir tikai
tā, ka no  pārdurtās apkārtnes ir jāņem tikai tie punkti
pārdurtās apkārtnes ir jāņem tikai tie punkti
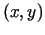 , kas apmierina saites vienādojumu.
, kas apmierina saites vienādojumu.
Piemēram, funkcijai 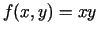 ekstrēma punktu nav. Ja izvēlas
saites vienādojumu
ekstrēma punktu nav. Ja izvēlas
saites vienādojumu 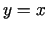 , tad
, tad  ir šīs funkcijas nosacītā
minimuma punkts. Ja saites vienādojums ir
ir šīs funkcijas nosacītā
minimuma punkts. Ja saites vienādojums ir 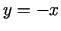 , tad
, tad  ir
funkcijas
ir
funkcijas 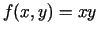 nosacītā maksimuma punkts.
nosacītā maksimuma punkts.
Funkcijas nosacītā ekstrēma punktu atrašanai lieto Lagranža
reizinātāju metodi, kura izriet no šādas teorēmas.
-
5.1. teorēma.
- (Nosacītā ekstrēma punkta
eksistences nepieciešamais nosacījums.)
Ja  ir funkcijas
ir funkcijas  nosacītā ekstrēma punkts
ar saites vienādojumu
nosacītā ekstrēma punkts
ar saites vienādojumu
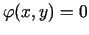 , tad eksistē tāds skaitlis
, tad eksistē tāds skaitlis 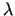 ,
ka punkts
,
ka punkts
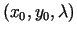 apmierina vienādojumu sistēmu
kur
apmierina vienādojumu sistēmu
kur
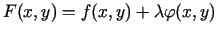 . Funkciju
. Funkciju 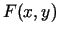 sauc
par Lagranža funkciju.
sauc
par Lagranža funkciju.
-
5.2. piezīme.
- Analoģiski definē triju argumentu funkcijas
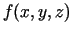 ar saites vienādojumu
ar saites vienādojumu
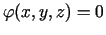 nosacītos ekstrēmus.
Lagranža funkcija šoreiz
nosacītos ekstrēmus.
Lagranža funkcija šoreiz
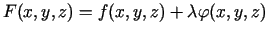 ,
bet sistēma nosacītā ekstrēma punkta atrašanai ir
,
bet sistēma nosacītā ekstrēma punkta atrašanai ir
-
5.1. piemērs.
- Lodē, kuras rādiuss ir
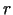 , ievilkt vislielākā tilpuma
paralēlskaldni.
, ievilkt vislielākā tilpuma
paralēlskaldni.
Apzīmē ar 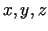 paralēlskaldņa šķautņu garumus. Tā tilpums
paralēlskaldņa šķautņu garumus. Tā tilpums
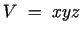 , bet diagonāle
, bet diagonāle 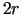 , pie tam
, pie tam
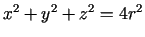 . Lai
atrastu funkcijas
. Lai
atrastu funkcijas 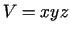 nosacītā maksimuma punktu ar saites
vienādojumu
nosacītā maksimuma punktu ar saites
vienādojumu
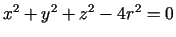 , sastāda Lagranža funkciju
Atrod
, sastāda Lagranža funkciju
Atrod
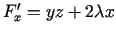 ,
,
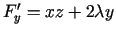 ,
,
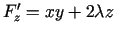 . Iegūst sistēmu
Šīs sistēmas atrisinājums
. Iegūst sistēmu
Šīs sistēmas atrisinājums 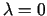 ,
,
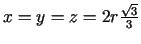 . Acīmredzami, kad
. Acīmredzami, kad
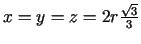 , funkcija
, funkcija 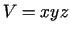 sasniedz vislielāko
vērtību. Šī vērtība ir
sasniedz vislielāko
vērtību. Šī vērtība ir
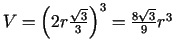 , bet
paralēlskaldnis ir kubs ar šķautni
, bet
paralēlskaldnis ir kubs ar šķautni
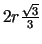 .
.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 5.1.1. Jautājumi
Augstāk: 5. PIELIKUMS
Iepriekšējais: 5. PIELIKUMS
2002-06-21
![]() plaknē nosaka vienības riņķa
līniju ar centru koordinātu sākuma punktā. Šis pats vienādojums telpā
nosaka cilindrisku virsmu ar veiduli, kas ir paralēla aplikātu asij.
plaknē nosaka vienības riņķa
līniju ar centru koordinātu sākuma punktā. Šis pats vienādojums telpā
nosaka cilindrisku virsmu ar veiduli, kas ir paralēla aplikātu asij.
![]() nosacītā minimuma punktu.
nosacītā minimuma punktu.
![]() ekstrēma punktu nav. Ja izvēlas
saites vienādojumu
ekstrēma punktu nav. Ja izvēlas
saites vienādojumu ![]() , tad
, tad ![]() ir šīs funkcijas nosacītā
minimuma punkts. Ja saites vienādojums ir
ir šīs funkcijas nosacītā
minimuma punkts. Ja saites vienādojums ir ![]() , tad
, tad ![]() ir
funkcijas
ir
funkcijas ![]() nosacītā maksimuma punkts.
nosacītā maksimuma punkts.
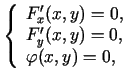
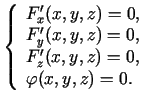
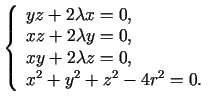
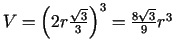 , bet
paralēlskaldnis ir kubs ar šķautni
, bet
paralēlskaldnis ir kubs ar šķautni