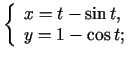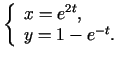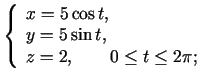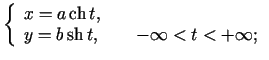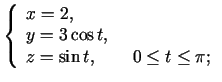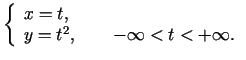Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: SATURS
Augstāk: 4. PARAMETRISKI UZDOTAS FUNKCIJAS UN VEKTORFUNKCIJAS
Iepriekšējais: 4.4. Jautājumi
- Pierādīt, ka vienādojumi
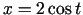 ,
,
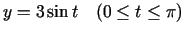 parametriski definē funkciju.
parametriski definē funkciju.
- Atrast
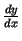 un
un
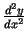 šādām
parametriski uzdotām funkcijām:
šādām
parametriski uzdotām funkcijām:
-
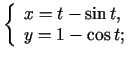
-
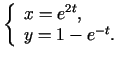
- Noskaidrot, kādu līniju telpā (vai plaknē)
uzdod šādi vienādojumi:
-
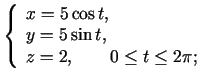
-
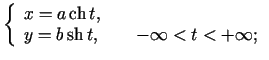
-
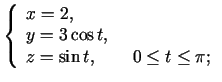
-
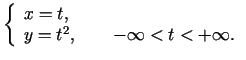
- Atvasināt šādas vektorfunkcijas un izskaitļot
atvasinājumu vērtības punktā
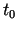 :
:
-
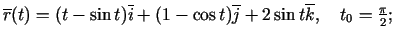
-
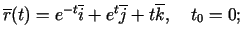
-
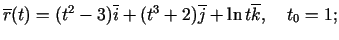
-
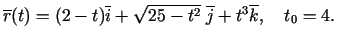



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: SATURS
Augstāk: 4. PARAMETRISKI UZDOTAS FUNKCIJAS UN VEKTORFUNKCIJAS
Iepriekšējais: 4.4. Jautājumi
2002-01-21