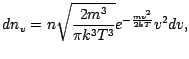Fizika DU TSC
Nākamais: 1.2. Vakuuma pakāpes Augstāk: 1. Vakuuma fizika Iepriekšējais: 1. Vakuuma fizika

1.1. Galvenie jēdzieni

Vakuums ir tāda gāzes retinājuma pakāpe, kad gāzes molekulu brīvā ceļa garums ir lielāks par trauka (kurā atrodas gāze) izmēriem. Skaitliski vakuumu raksturo kā starpību starp atmosfēras spiedienu un absolūto spiedienu vakuumsistēmā. Tāpēc vakuumu mērā tādās pašās mērvienībās kā spiedienu.

Galvenie jēdzieni vakuumfizikā tiek balstīti uz šādām molekulāri - kinētiskās teorijas hipotēzēm:

• gāze ir molekulu kopa, kuras nepārtraukti un haotiski kustās;
• mijiedarbība starp molekulām notiek tikai tām saduroties, pie tam sadursmes ir absolūti elastīgas;
• siltums ir mehāniskās enerģijas forma - molekulu kinētiskā enerģija;
• eksistē laikā konstants molekulu sadalījums pa ātrumiem;
• gāze ir izotropa.

Izmantojot šīs hipotēzes, var iegūt gāzes molekulu sadalījuma pa ātrumiem funkciju - Maksvela-Bolcmaņa sadalījumu :

$$dn_v=n\sqrt{\frac{2m^3}{\pi k^3T^3}}e^{-\frac{mv^2}{2kT}}v^2dv,$$ (1.1)

kur $dn_v$ - molekulu skaits ar ātrumiem intervālā no $v$ līdz $v+dv$; $n$ - molekulu skaits tilpuma vienībā; $m$ - molekulas massa; $k$ - Bolcmaņa konstante; $T$ - absolūtā temperatūra.

Sadalījuma funkcijai (1.1) maksimums ir tad, ja

$$v_{var}=\sqrt{\frac{2kT}{m}}.$$

Šo ātrumu sauc par visvarbūtīgāko molekulu ātrumu. Zīmējumā 1.1. ir redzama slāpekļa sadalījuma funkcija.

1.1. zīmējums. Slāpekļa sadalījuma funkcija.
1 - $T=25^\circ$C, 2 - $T=400^\circ$C.

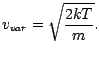
Izņemot visvarbūtīgāko ātrumu, var atrast arī vidējo aritmētisko molekulu ātrumu

$$v_{ar}=\frac{1}{n}\int\limits_0^\infty vdn_v=\sqrt{\frac{8kT}{\pi m}},$$ (1.2)

un vidējo kvadrātisko molekulu ātrumu

$$v_{kv}==\sqrt{\frac{1}{n}\int\limits_0^\infty v^2dn_v}=\sqrt{\frac{3kT}{m}}.$$ (1.3)

Formulu, molekulu spiediena vai mijiedarbības spēka ar vakuumkameras sienas laukuma vienību izskaitļošanai, var iegūt izmantojot divas pirmās hipotēzes un otro Ņūtona likumu :

$$p=\frac{mnv^2_{kv}}{3}=\frac{\rho v^2_{kv}}{3},$$ (1.4)

kur $\rho$ - gāzes blīvums, $\rho=mn$.

Ja kamerā atrodas dažādu gāzu maisījums, tad, lai noteiktu spiediena lielumu, ir nepieciešams atrast visu maisījuma molekulu kustības daudzuma (impulsa) izmaiņu laika vienībā:

$$p_{mais}=\sum\limits_{j=1}^K \frac{1}{3}m_jn_jv_j^2,$$ (1.5)

kur $m_j$, $n_j$, $v_j$ - $j$-tās gāzes molekulu massa, koncentrācija un vidējais kvadrātiskais ātrums atbilstoši, $K$ - maisījuma gāzu skaits. No (1.4) un (1.5) var iegūt:

$$p_{mais}=\sum\limits_{j=1}^K p_j.$$ (1.6)

Izteiksmi (1.6) sauc par Daltona likumu: savstarpēji ķīmiski nereaģējušu gāzu maisījuma kopīgais spiediens ir atsevišķu maisījuma gāzu parciālo spiedienu summa.

Vienādojumus (1.5) un (1.6) var izmantot tikai gadījumā, kad izpildās pirmās divas molekulāri - kinētiskās teorijas hipotēzes par molekulu vienādi varbūtīgu kustību un elastīgām sadursmēm ar kameras sienām. Ļoti zemu spiedienu apgabalā šie nosacījumi neizpildās.

Izmantojot molekulu sadalījumu pa ātrumiem (1.1) var iegūt arī tādu vakuumtehnikā svarīgu lielumu, kā molekulu skaitu, kas laika vienībā triecas pret kameras sienas laukuma vienību:

$$N_q=\frac{n v_{ar}}{4}.$$ (1.7)

Praktiski bieži ir svarīgāk zināt nevis molekulu skaitu $N_q$, bet gāzes tilpumu $V_q$ litros, ko aizņem molekulas, kuras vienā laika vienībā triecas pret kameras sienas laukuma vienību. Tad (1.7) abas puses izdalam ar $n$ un iegūsim:

$$V_q=\frac{v_{ar}}{4}=36,38 \sqrt{\frac{T}{M}}, ^2 \cdot .$$ (1.8)

kur $M$ - gāzes molmasa. Acīmredzami, gāzes tilpums, kas vienā laika vienībā trieksies uz kameras laukumu $A$ (m$^2$), būs:

$$V_A=36,38 A\sqrt{\frac{T}{M}}, .$$ (1.9)

Formulu (1.8) praktiski izmanto lai noteiktu tvaika strūklas sūkņu, dažādu slazdu, sorbcijas sūkņu ātrdarbību u.c.

Izplatītākā vakuuma mērvienība ir dzīvsudraba staba milimetri jeb Torr - Toričelli . 1 mmHg (Torr) ir spiediens, ko rada 1 mm augsts dzīvsudraba stabs, ja dzīvsuraba blīvums ir 13595,1 kg/m$^3$ (pie $t=0^\circ$C) un brīvās krišanas paātrinājums ir normāls - 9,80665 m/s$^2$. 1 Torr=133,32239 N/m$^2$.

Fizika DU TSC
Nākamais: 1.2. Vakuuma pakāpes Augstāk: 1. Vakuuma fizika Iepriekšējais: 1. Vakuuma fizika