


 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.2. Punktā nepārtraukta funkcija
Augstāk: 2. VAIRĀKU ARGUMENTU FUNKCIJAS ROBEŽA UN
Iepriekšējais: 2. VAIRĀKU ARGUMENTU FUNKCIJAS ROBEŽA UN
Vairāku argumentu funkciju
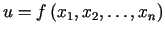 bieži pieraksta kā
bieži pieraksta kā 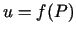 , kur
, kur
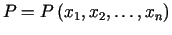 . Šāds funkcijas pieraksts ir
izdevīgs, definējot funkcijas
. Šāds funkcijas pieraksts ir
izdevīgs, definējot funkcijas 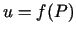 robežu punktā
robežu punktā
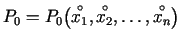 .
(Definīcija atgādina viena argumenta funkcijas galīgās robežas
definīciju punktā
.
(Definīcija atgādina viena argumenta funkcijas galīgās robežas
definīciju punktā  , kur
, kur  - reāls skaitlis). Attālumu starp
punktiem
- reāls skaitlis). Attālumu starp
punktiem  un
un  apzīmē ar
apzīmē ar
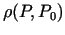 2.1. Definējot funkcijas robežu punktā
2.1. Definējot funkcijas robežu punktā  , vienojas uzskatīt, ka
funkcija ir definēta šī punkta kaut kādā apkārtnē, izņemot varbūt
pašu punktu
, vienojas uzskatīt, ka
funkcija ir definēta šī punkta kaut kādā apkārtnē, izņemot varbūt
pašu punktu  .
.
-
2.1. definīcija.
- Skaitli
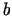 sauc par funkcijas
sauc par funkcijas 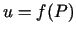 robežu punktā
robežu punktā  , ja jebkuram
, ja jebkuram
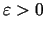 eksistē tāds
eksistē tāds 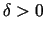 (atkarīgs no
(atkarīgs no
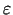 ), ka visiem
), ka visiem
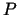 , kuriem
, kuriem
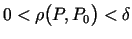 , izpildās nevienādība
, izpildās nevienādība
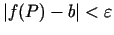 . Pieraksta:
. Pieraksta:
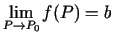
jeb
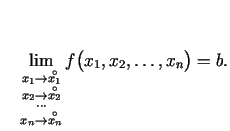
Ja par taisnes punkta 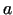
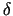 - apkārtni sauc vaļēju
intervālu
- apkārtni sauc vaļēju
intervālu
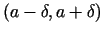 , tad par plaknes punkta
, tad par plaknes punkta
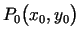
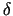 - apkārtni sauc vaļēju riņķi (bez
riņķa līnijas punktiem) ar centru punktā
- apkārtni sauc vaļēju riņķi (bez
riņķa līnijas punktiem) ar centru punktā
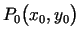 un
rādiusu
un
rādiusu 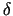 (2.1. zīm.). Analoģiski par telpas punkta
(2.1. zīm.). Analoģiski par telpas punkta
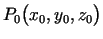
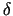 - apkārtni sauc vaļēju lodi
(bez sfēras punktiem) ar centru šajā punktā un rādiusu
- apkārtni sauc vaļēju lodi
(bez sfēras punktiem) ar centru šajā punktā un rādiusu 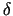 (2.2. zīm.).
(2.2. zīm.).
Ja no punkta  apkārtnes ir izņemts punkts
apkārtnes ir izņemts punkts  , tad šādu kopu
sauc par punkta
, tad šādu kopu
sauc par punkta  pārdurto apkārtni. Punkta
pārdurto apkārtni. Punkta 
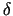 - apkārtni var uzdot ar nevienādību
- apkārtni var uzdot ar nevienādību
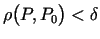 , bet šī punkta pārdurto
, bet šī punkta pārdurto
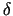 - apkārtni var uzdot ar divkāršu nevienādību
- apkārtni var uzdot ar divkāršu nevienādību
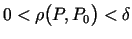 .
.
Izmantojot punkta 
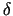 - apkārtni,
2.1. definīciju var formulēt šādi.
- apkārtni,
2.1. definīciju var formulēt šādi.
-
2.2. definīcija.
- Skaitli
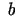 sauc par funkcijas
sauc par funkcijas
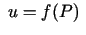 robežu punktā
robežu punktā 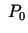 , ja jebkuram
, ja jebkuram
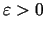 eksistē tāda punkta
eksistē tāda punkta 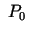 pārdurtā
pārdurtā 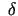 - apkārtne, ka
visiem
- apkārtne, ka
visiem  no šīs apkārtnes izpildās nevienādība
no šīs apkārtnes izpildās nevienādība
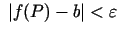 .
.
-
2.1. piezīme.
-

- No 2.2. definīcijas seko, ka
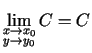 (robeža no konstantes ir pati konstante),
(robeža no konstantes ir pati konstante),
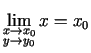 un
un
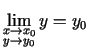 .
.
- Tā kā vairāku argumentu funkcijas robežas definīcija ir
analoģiska viena argumenta funkcijas galīgās robežas definīcijai,
tad ir spēkā teorēmas, kas analoģiskas teorēmām par viena argumenta
funkciju galīgām robežām. Pierādījumi arī ir analoģiski.
-
2.1. teorēma.
- (Robežas
vienīgums).
Ja funkcijai 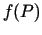 punktā
punktā  eksistē robeža, tad vienīgā
veidā.
eksistē robeža, tad vienīgā
veidā.
-
2.2. teorēma.
- Ja funkcijai
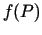 punktā
punktā  eksistē robeža, tad funkcija ir ierobežota šī punkta kaut kādā
apkārtnē.
eksistē robeža, tad funkcija ir ierobežota šī punkta kaut kādā
apkārtnē.
-
2.3. teorēma.
- (Par robežpāreju
nevienādībās).
Ja eksistē
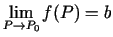 ,
,
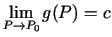 un punkta
un punkta  kaut kādā
pārdurtajā apkārtnē izpildās nevienādība
kaut kādā
pārdurtajā apkārtnē izpildās nevienādība 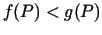 , tad
, tad 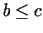 .
.
- Sekas.
- Ja eksistē
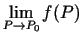 un
punktā
un
punktā  kaut kādā pārdurtajā apkārtnē
kaut kādā pārdurtajā apkārtnē 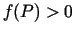 , tad
, tad
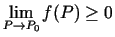 .
.
-
2.4. teorēma.
- (Mainīgā starplieluma
robeža).
Ja eksistē
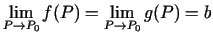 un punkta
un punkta  kaut kādā pārdurtajā apkārtnē izpildās nevienādība
kaut kādā pārdurtajā apkārtnē izpildās nevienādība
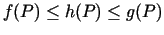 , tad eksistē arī
, tad eksistē arī
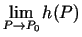 un tā ir vienāda ar
un tā ir vienāda ar 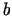 .
.
-
2.5. teorēma.
- (Aritmētiskās darbības ar
robežām).
Ja eksistē
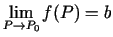 un
un
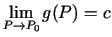 , tad eksistē arī
robežas šo funkciju summai, starpībai, reizinājumam un dalījumam (dalījuma
gadījumā
, tad eksistē arī
robežas šo funkciju summai, starpībai, reizinājumam un dalījumam (dalījuma
gadījumā 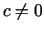 ), pie tam
), pie tam
-
2.3. definīcija.
- Funkciju
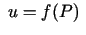 sauc par bezgalīgi
mazu, kad
sauc par bezgalīgi
mazu, kad
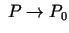 , ja
, ja
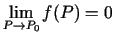 .
.
-
2.1. piemērs.
- Izskaitļot
-
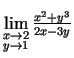 ;
;
-
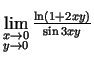 .
.
- Izmanto 2.5. teorēmu, robežu no konstantes un to, ka
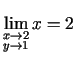 ,
,
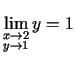 .
.
- Apzīmē
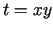 . Ja
. Ja
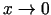 un
un
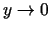 , tad
, tad
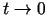 .
.
-
2.2. piezīme.
- Vairāku argumentu funkcijas robeža (protams, ja tā
eksistē) nav atkarīga no virziena, kādā punkts
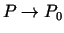 (nav svarīga arī līknes, pa kuru
(nav svarīga arī līknes, pa kuru
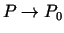 , forma). Ja
punktam
, forma). Ja
punktam 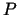 tiecoties uz punktu
tiecoties uz punktu  no dažādām pusēm, funkcijas
no dažādām pusēm, funkcijas
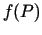 vērtības tiecas uz dažādiem skaitļiem, tad robeža punktā
vērtības tiecas uz dažādiem skaitļiem, tad robeža punktā
 neeksistē.
neeksistē.
-
2.2. piemērs.
- Parādīt, ka neeksistē
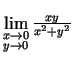 .
.
Lai punkts 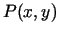 tuvojas uz
tuvojas uz 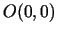 pa taisni
pa taisni 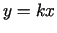 . Ja
. Ja
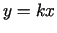 , tad
, tad
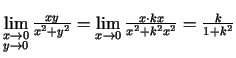 . Acīmredzami šī vērtība
. Acīmredzami šī vērtība
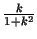 ir atkarīga no taisnes
ir atkarīga no taisnes 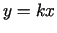 virziena koeficienta
virziena koeficienta
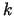 . Tādējādi
. Tādējādi
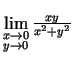 neeksistē.
neeksistē.
-
2.3. piemērs.
- Izskaitļot
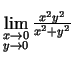 .
.
Apzīmē
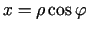 un
un
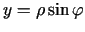 , kur
, kur 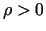 .
Tā kā
.
Tā kā
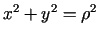 , tad
, tad
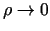 , kad
, kad
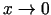 un
un
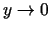 . Neatkarīgi no leņķa
. Neatkarīgi no leņķa
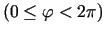 izvēles
izvēles
Tādējādi
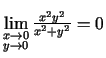 . (Šoreiz 2.5. teorēmu pielietot nedrīkst, jo
. (Šoreiz 2.5. teorēmu pielietot nedrīkst, jo
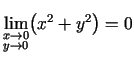 ).
).
-
2.3. piezīme.
- Paņēmienu, kurš izmantots 2.3. piemērā,
bieži izmanto divu argumentu funkciju robežu izskaitļošanai.



 Matemātika
DU TSC
Matemātika
DU TSC
Nākamais: 2.2. Punktā nepārtraukta funkcija
Augstāk: 2. VAIRĀKU ARGUMENTU FUNKCIJAS ROBEŽA UN
Iepriekšējais: 2. VAIRĀKU ARGUMENTU FUNKCIJAS ROBEŽA UN
2002-06-21
![]() bieži pieraksta kā
bieži pieraksta kā ![]() , kur
, kur
![]() . Šāds funkcijas pieraksts ir
izdevīgs, definējot funkcijas
. Šāds funkcijas pieraksts ir
izdevīgs, definējot funkcijas ![]() robežu punktā
robežu punktā
![]() .
(Definīcija atgādina viena argumenta funkcijas galīgās robežas
definīciju punktā
.
(Definīcija atgādina viena argumenta funkcijas galīgās robežas
definīciju punktā ![]() , kur
, kur ![]() - reāls skaitlis). Attālumu starp
punktiem
- reāls skaitlis). Attālumu starp
punktiem ![]() un
un ![]() apzīmē ar
apzīmē ar
![]() 2.1. Definējot funkcijas robežu punktā
2.1. Definējot funkcijas robežu punktā ![]() , vienojas uzskatīt, ka
funkcija ir definēta šī punkta kaut kādā apkārtnē, izņemot varbūt
pašu punktu
, vienojas uzskatīt, ka
funkcija ir definēta šī punkta kaut kādā apkārtnē, izņemot varbūt
pašu punktu ![]() .
.
![]()
![]() - apkārtni sauc vaļēju
intervālu
- apkārtni sauc vaļēju
intervālu
![]() , tad par plaknes punkta
, tad par plaknes punkta
![]()
![]() - apkārtni sauc vaļēju riņķi (bez
riņķa līnijas punktiem) ar centru punktā
- apkārtni sauc vaļēju riņķi (bez
riņķa līnijas punktiem) ar centru punktā
![]() un
rādiusu
un
rādiusu ![]() (2.1. zīm.). Analoģiski par telpas punkta
(2.1. zīm.). Analoģiski par telpas punkta
![]()
![]() - apkārtni sauc vaļēju lodi
(bez sfēras punktiem) ar centru šajā punktā un rādiusu
- apkārtni sauc vaļēju lodi
(bez sfēras punktiem) ar centru šajā punktā un rādiusu ![]() (2.2. zīm.).
(2.2. zīm.).
![]() apkārtnes ir izņemts punkts
apkārtnes ir izņemts punkts ![]() , tad šādu kopu
sauc par punkta
, tad šādu kopu
sauc par punkta ![]() pārdurto apkārtni. Punkta
pārdurto apkārtni. Punkta ![]()
![]() - apkārtni var uzdot ar nevienādību
- apkārtni var uzdot ar nevienādību
![]() , bet šī punkta pārdurto
, bet šī punkta pārdurto
![]() - apkārtni var uzdot ar divkāršu nevienādību
- apkārtni var uzdot ar divkāršu nevienādību
![]() .
.
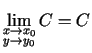 (robeža no konstantes ir pati konstante),
(robeža no konstantes ir pati konstante),
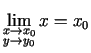 un
un
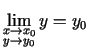 .
.
![]() punktā
punktā ![]() eksistē robeža, tad vienīgā
veidā.
eksistē robeža, tad vienīgā
veidā.
![]() ,
,
![]() un punkta
un punkta ![]() kaut kādā
pārdurtajā apkārtnē izpildās nevienādība
kaut kādā
pārdurtajā apkārtnē izpildās nevienādība ![]() , tad
, tad ![]() .
.
![]() un punkta
un punkta ![]() kaut kādā pārdurtajā apkārtnē izpildās nevienādība
kaut kādā pārdurtajā apkārtnē izpildās nevienādība
![]() , tad eksistē arī
, tad eksistē arī
![]() un tā ir vienāda ar
un tā ir vienāda ar ![]() .
.
![]() un
un
![]() , tad eksistē arī
robežas šo funkciju summai, starpībai, reizinājumam un dalījumam (dalījuma
gadījumā
, tad eksistē arī
robežas šo funkciju summai, starpībai, reizinājumam un dalījumam (dalījuma
gadījumā ![]() ), pie tam
), pie tam
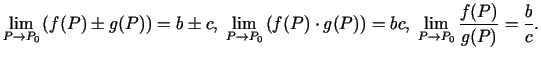
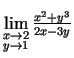 ;
;
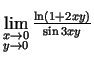 .
.
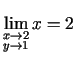 ,
,
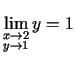 .
.
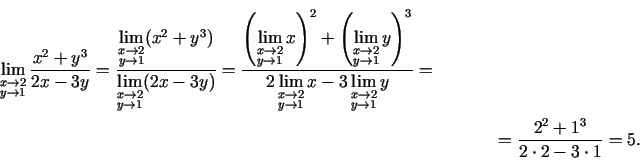
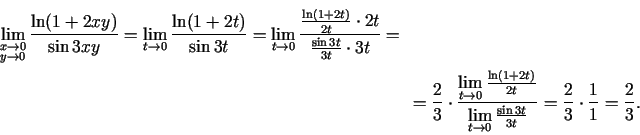
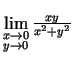 .
.
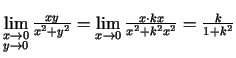 . Acīmredzami šī vērtība
. Acīmredzami šī vērtība
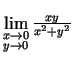 neeksistē.
neeksistē.
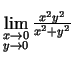 .
.
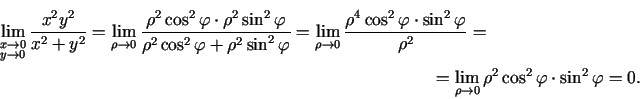
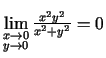 . (Šoreiz 2.5. teorēmu pielietot nedrīkst, jo
. (Šoreiz 2.5. teorēmu pielietot nedrīkst, jo
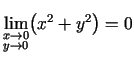 ).
).